ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ ПАРНОГО ВЗАИМОДЕЙСТВИЯ МЕТАНСОДЕРЖАЩИХ БИНАРНЫХ СИСТЕМ УРАВНЕНИЯ СОСТОЯНИЯ ПЕНГА-РОБИНСОНА

Методы прогнозирования и анализа фазового состояния и PVT-свойств природных газов и нефтей основываются на комплексном использовании результатов промысловых измерений, лабораторных исследований и математического моделирования соответствующих процессов. В качестве базового аппарата в инженерных расчетах используются уравнения состояния, законы термодинамики многокомпонентных систем и эффективные вычислительные процедуры. В практике технологических расчетов для оценки свойств газов и жидкостей применяют также и апробированные корреляции, которые приводятся в учебной и научно-методической литературе.

Уравнение состояния Пенга – Робинсона (PR) и его модификации без соответствующей коррекции коэффициентов парного взаимодействия количественно не описывают равновесие в углеводородных системах

где R=0,0083144 МПа^.м³/(кмоль^.К) – универсальная газовая постоянная, коэффициенты уравнения для чистого вещества являются функциями критической температуры , критического давления  и ацентрического фактора :

Для многокомпонентной смеси уравнение описывает поведение газа или жидкости, в гетерогенной области, а коэффициенты уравнения рассчитываются по правилам смешения:

                                                         (11)

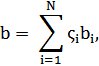                                                                                            (12)

где N – общее число компонентов смеси; i – номер компонента; z_i — мольная доля i-го компонента в соответствующей фазе; C_ij –коэффициенты парного взаимодействия i-го и j-го компонентов смеси, уточняющие правила смешения и введены главным образом для того чтобы, избежать перекрёстного взаимодействия и полярности между компонентами смеси и позволяют повысить точность расчетов фазового равновесия.

Для описания фазового равновесия в этих системах необходимо использовать специальную процедуру коррекции коэффициентов парного взаимодействия, представляя последние как функции основных параметров процесса.

Алгоритм поиска коэффициентов парного взаимодействия основан на определении значений КПВ для экспериментальных составов фаз на каждой изотерме, для которых выполняется равенство [1,2]:

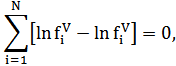
где и f_i^V, f_i^L – летучести компонентов  бинарной смеси в паровой и жидкой фазах соответственно; N – число экспериментальных точек на изотерме.

Экспериментальные данные выбираются из открытых источников. Составы паровой и жидкой фаз для упомянутых бинарных систем, как правило, определялись в различных экспериментах при разных термобарических условиях. Но для расчета КПВ необходимы данные по составам равновесных фаз бинарных смесей при одних и тех же значениях давлений и температур. Поэтому экспериментальные данные по составу одной из фаз дополнялись данными, полученными интерполяцией экспериментальных значений функциями температуры и давления, при термобарических условиях, для которых уже существуют экспериментальные значения состава другой фазы. Система уравнений решалась методом Ньютона. При необходимости для уточнения в определенной окрестности полученных значений КПВ использовался перебор с шагом 0,0001 с расчетом следующего функционала:

где x_i^E и y_i^E – экспериментальные значения растворимости компонентов природного газа в жидкой и паровой фазе, соответственно, при i-ом давлении; x_i^C и y_i^C – значения растворимости компонента природного газа в жидкой и паровой фазе соответственно при i-ом давлении, полученные по результатам расчета парожидкостного равновесия при проверяемых значениях КПВ. Таким образом, для каждой изотермы получены значения КПВ для жидкой и паровой фаз, которые были аппроксимированы температурными зависимостями.

В результате получены температурные зависимости коэффициента парного взаимодействия азота с рядом углеводородов, полученные научным коллективом под руководством Ю.В. Калиновского Таблица 1.

Таблица 1.

Зависимости от температуры для коэффициента парного взаимодействия

В Таблице 1 в первом столбце представлен компонент, во втором функция зависимости для относительной температуры (T/100), в третьем интервал температуры в котором определись функциональная зависимость, в четвертом относительная погрешность при постоянном значении коэффициента парного взаимодействия , в пятом относительная погрешности для переменного коэффициента парного взаимодействия , в шестом относительное погрешность между постоянным и переменном значением коэффициента парного взаимодействия .

Из Таблицы 1 видно, что функциональная зависимость коэффициента парного взаимодействия от температуры для метана аппроксимируется кривой второго порядка. Анализ погрешностей показывает, что снижение относительных ошибок расчета существенен и в промышленных масштабах может привести к значительным энергетическим и экономическим потерям.

Использованные источники:

1. Брусиловский А.И. – Фазовые превращения при разработке месторождений нефти и газа. – М. : Издательский дом «Грааль», 2002.

2. Калиновский Ю.В., Пономарев А.И. – Двухфазные и трехфазные равновесия в газодобыче. – Уфа, 2006.