Новые технологии не стоят на месте и скорости передачи данных растут. На ранних стадиях развития технологий не учитывалась поляризационная модовая дисперсия так, как она вносила малое влияние на передаваемый сигнал, но с ростом скорости передачи ее влияние увеличивается.
В данной статье исследуется влияние ПМД на сигналы современной волоконно-оптической системы передачи, рассматривается ее природа возникновения и методы борьбы с ней.
ПМД возникает из-за анизотропии вещества или двулучепреломления. Изменение свойств среды обусловлено влиянием внешних факторов на оптический кабель, его скрутка, вытягивание, смещение центра и т.д.. ПМД сдерживает дальнейшее увеличение скорости и дальность передачи по волоконно-оптическим линиям связи. Это значит, что требуется очень щепетильная работа, качественная прокладка волокна в грунт, применение специального оптического волокна и использование помехоустойчивого кодирования.
Математическая модель – математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе. Математическая модель предназначена предсказать поведение реального объекта, но всегда представляет собой ту или иную степень его идеализации.
Рассмотрим известные и хорошо апробированные математические модели, учитывающие влияние ПМД в волоконно-оптических линейных трактах.
Существует 5 решений таких моделей:
1) Решение Р.Л.Фримана;
2) Решение Р.Р.Убайдулаева;
3) Решение И.П.Каминова;
4) Решение Г.П.Агравала;
5) Решение А.К.Григоряна.
Рассмотрим каждый из них.
1. Решение Фримана
По Фриману, благодаря ПМД возникает межсимвольная интерференция, которая приводит к ухудшению показателей системы около 1 дБ (с учетом хроматической дисперсии). Часть ПМД составляет 0,1Тб.
Влияние ПМД возрастает:
– с увеличением скорости передачи в канале;
– с увеличением длины линии (количество усилителей и компенсаторов ХД);
– с увеличением числа каналов.
В данном решении дисперсия может составлять 0,4 Тб (суммарная дисперсия: хроматическая и поляризационная модовая). Это исходит из выражения:
![]() , (1)
, (1)
где Т0 – первоначальная ширина импульса;
Т1 – ширина импульса, на котором проводились измерения.
при L/L д= 0,9616, где L-длина линии и L д – дисперсионная длина. С учетом ПМД L/Lд =0,98.
![]() (2)
(2)
где ![]() – среднеквадратическая длительность импульса.
– среднеквадратическая длительность импульса.
В этом случае Т1/То=0,269 дБ.
2. Решение Убайдулаева
В данном методе ПМД определяется:
![]() (3)
(3)
Удельная полоса пропускания:
W = 0,44/D (4)
Определив хроматическую дисперсию, определим поляризационную модовую дисперсию:
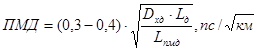 (5)
(5)
3. Решение Каминова
Более новый метод позволяет определить дисперсию, в котором норма ПМД не превышает вносимых потерь (не более 1 дБ).
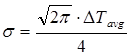 (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Согласно документу МСЭ-Т G.691 допустимая норма на ПМД не должна превышать 0,1Тб или 0,2828То.
4. Решение Агравала
Агравал вывел формулу для нахождения допустимого изменения гауссовского импульса по ПМД:
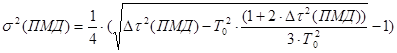 (10)
(10)
Здесь ∆τ(ПМД) – среднее значение ПМД пс, Т0 – полуширина гауссовского импульса по уровню 1/е, пс.
В результате получаем σ(ПМД)=0,375 и Т0=0,1325Тб.
Принимаем ∆τ(ПМД) = Т0. В результате получаем σ (ПМД) = 0,145Тб.
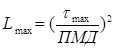 (11)
(11)
![]() (12)
(12)
5. Решение Григоряна
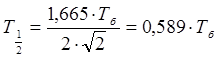 (13)
(13)
Необходимо подчеркнуть, что ПМД зависит от формы импульса, так как потери связаны со значениями ПМД и зависят от этой формы, так для формата модуляции NRZ
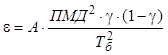 (14)
(14)
где А – параметр, зависящий от формы импульса и характеристик приемного фильтра (таблица 1).
|
Форма импульса |
А |
|
Гауссовский |
25 |
|
Прямоугольный |
12 |
|
Треугольный |
24 |
Таблица 1 – Значения А для различных форм импульса
Для того, чтобы сохранить потери по дисперсии в 1 дБ, необходимо уменьшить расстояние между усилителями и, тем самым увеличить среднее значение ПМД за счет дополнительных усилителей и компенсаторов хроматической дисперсии. Однако, если не уменьшать допустимую длину и оставить решения по длине на уровне хроматической дисперсии, то мы получим увеличение потерь по затуханию за счет поляризационной модовой дисперсии (ПМД) и большее значение уширения импульса.
Согласно полученным результатам ПМД составляет 9–10 % от значения дисперсии групповых скоростей. Эти решения получили подтверждение в работах Агравала.
Таким образом, рассмотрены математические модели в линейных волоконно-оптических трактах, которые учитывают поляризационную модовую дисперсию. К сожалению, на сегодняшний день не изобретены способы ее уменьшения, но есть способ увеличения скорости путем использования многопозиционных и многомерных типов модуляции.
Список литературы:
1. Песков, С.Н. Поляризационная модовая дисперсия в оптическом волокне [Электронный ресурс] / С.Н. Песков, А.И. Барг, И.А. Колпаков // URL: http://www.konturm.ru/download/stat/2005/281105.pdf (дата обращения 05.11.2019)
2. Саитов, И.А. Физические основы построения волоконно-оптических систем передачи информации / И.А. Саитов, В.Т. Ерёменко, А.П. Фисун, Д.Ю. Музалевский, К.И. Мясин. – Орёл : ОГУ им. И.С. Тур-генева, РГГУ, 2017. – 502 с
3. Убайдуллаев, Р.Р. Волоконно-оптические сети / Р.Р. Убайдуллаев. – М. : Эко-Трендз, 2007. – 267 с.
4. Фриман, Р.Л. Волоконно-оптические системы связи / Р.Л. Фриман ; перевод с анг. / Под ред. Н. Н. Слепова – М. : Техносфера, 2003. – 590 с.
5. Агравал, Г.П. Нелинейная волоконная оптика / Г.П. Агравал : перевод с англ. С.В. Черникова и др. / Под ред. П.В. Мамышева. – М. : Мир, 1996. – 323 с.

