Геометрия Лобачевского основана на тех же основных аксиомах, что и, привычная нам, Евклидова геометрия, за исключением аксиомы о параллельных. В геометрии Евклида принимается за аксиому, что через точку, не лежащую на прямой, проходит в точности одна параллельная прямая. А в геометрии Лобачевского принимается аксиома, что через эту точку проходит, по крайней мере, две различные параллельные прямые.
Данная статья будет интересна студентам математических дисциплин. Рассматриваемые простейшие вопросы дадут понимание пространств, отличных от евклидового, помогут избавиться от евклидовых стереотипов.
Для школьников статья полезна, как для расширения кругозора, так и для лучшего понимания темы «построение циркулем и линейкой». Польза от навыков построения на плоскости Лобачевского, такая же, как от освоения тем «построения одним циркулем» или «построение одной линейкой». Рассмотрение вопросов построения неклассическим способом (на плоскости Лобачевского, одним циркулем или одной линейкой) позволит лучше понять саму проблематику задач на построение в стандартной интерпретации.
Отдельно хочется отметить провалы в освоение школьниками темы «задачи на построение». В том числе, данное негативное явление произошло из-за отсутствия таких задач в ЕГЭ. В то же время, трудно переоценить пользу от освоения этой темы. Она так же полезна, как экспериментальные занятия на уроках химии или физики. Выполнение задач на построение требует от учеников конкретных действий, позволяет связать теоретические вопросы с практической реализацией.
Написанное выше дает обоснование актуальности заявленной темы и предваряет несколько статей, в которых будут рассмотрены основные, базовые задачи на построение в плоскости Лобачевского. Такие как, провести прямую через две точки, построить перпендикуляр из заданной точки на заданную прямую, провести прямую через заданную точку в заданном направлении и т.д.
Помимо изучения и приобретения навыков решения задач в плоскости Лобачевского, на любую рассматриваемую задачу всегда можно посмотреть привычными «евклидовыми» глазами. Тем самым мы получим классическую задачу, решение которой подскажут интерпретации из плоскости Лобачевского. Для иллюстрации последнего тезиса, предлагаем решить следующую задачу.
Задача. Построить на плоскости точку равноудаленную от заданной окружности и двух заданных точек вне окружности.
Если читателю не охота решать задачу самостоятельно или решить задачу не удалось, приводим свое решение.
Прежде всего, напомним определение преобразования инверсии относительно окружности. Пусть на плоскости задана окружность с центром в точке O. Преобразование инверсии относительно заданной окружности однозначно определяет образ (точка Y) и прообраз (точка X) по следующему правилу: векторы OX и OY коллинеарны и сонаправлены, конкретное место точек на прямой ОХУ поясняет рисунок:
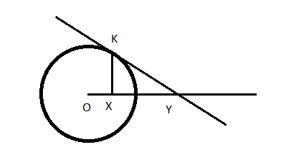
Т.е. чтобы найти Y по X, нужно из точки X восстановить перпендикуляр к ОХ до пересечения с окружностью (точка K), точку Y получим как пересечение касательной в точке K и OX. А чтобы найти точку X по Y, нужно из Y провести касательную и из точки касания опустить перпендикуляр на OY. Отметим, что при инверсии точки, лежащие на окружности, остаются неподвижными, а точка O не имеет образа (условно считаем, что образ O – бесконечная точка). При инверсии прямые, проходящие через O, переходят сами в себя. Остальные прямые, переходят в окружности, проходящие через O (в точку O переходят бесконечно удаленные точки прямой) и наоборот. Остальные окружности (не проходящие через центр) переходят в окружности. Окружность переходит сама в себя тогда и только тогда, когда окружность перпендикулярна окружности, относительно которой производится преобразование инверсии. Важным свойством инверсии является конформность – сохранение углов между прямыми и другими линиями (нас будут интересовать окружности).
Решение. Пусть A и B – заданные точки и α – заданная окружность. Понятно, что искомая точка является центром окружности, проходящей через точки A, B и касающуюся заданную окружность α. Таким образом, для решения задачи достаточно построить точку K – точку касания этих двух окружностей.
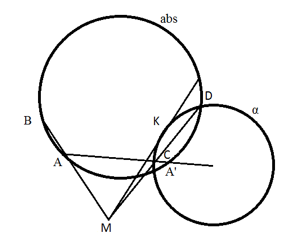
Построим точку A’ – образ точки A при инверсии относительно окружности α. Через точки A, B, A’ проведем окружность abs. Пусть точки окружности α и abs пересекаются в точках C и D и пусть M – точка пересечения прямых AB и CD. Проведем из M касательную к α так, чтобы точка касания K лежала внутри окружности abs (т.е. возьмем из двух возможных точек касания ту, что лежит внутри окружности abs). Точка K – искомая.
Для того чтобы пояснить, почему выполнялись именно эти построения и почему данные построения верны, дадим описание одной из интерпретаций плоскости Лобачевского. А именно, модели Пуанкаре плоскости Лобачевского в круге. За модель плоскости Лобачевского выбирается любой круг в плоскости. Точки окружности, ограничивающей выбранный круг, считаются бесконечно удаленными. Поэтому окружность называют абсолютом. За прямые принимаются окружности, перпендикулярные абсолюту. Проверено, что в такой модели выполняются все аксиомы плоскости Лобачевского.
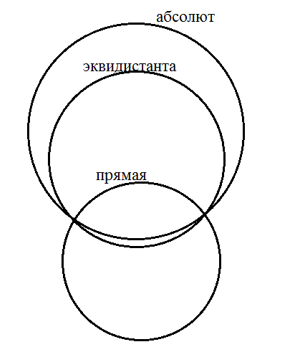
Приведем еще один объект из плоскости Лобачевского. Зафиксируем прямую и поднимем каждую точку прямой на одно и то же расстояние. В евклидовой плоскости получилось бы прямая, параллельная фиксированной. В плоскости Лобачевского получится некоторая линия, которая называется эквидистантой к прямой. На модели Пуанкаре эквидистанта изобразится окружностью, проходящей через те же точки абсолюта, что и фиксированная прямая.
Для пояснения построения проведем еще две окружности – окружность β через точки A и B, перпендикулярную abs и окружность γ с центром в точке M и радиусом MK.
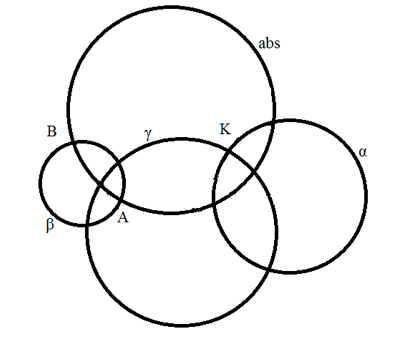
Теперь на окружность abs, можно посмотреть, как на абсолют в модели Пуанкаре плоскости Лобачевского в круге. Тогда окружности α, β и γ будут изображать прямые в плоскости Лобачевского. Причем прямая γ является единственным общим перпендикуляром прямых α и β. Поэтому окружность, проходящая через точки A, B и K, является эквидистантой к окружности β и касается окружности α (т.к. K – единственная на α точка, ближайшая к β, как основание общего перпендикуляра).
Литература
- Вернер А.Л. О бесконечных полных выпуклых поверхностях в пространстве Лобачевского // Известия ВУЗов. Математика. – 1960. – № 6 – С. 50-61.

