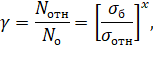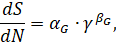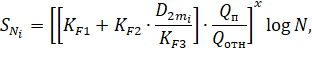Из-за сложности механизмов
ухудшения характеристик пути в вертикальной плоскости, построение точной
математической модели пути является трудной задачей. Множество исследователей
внесли значительный вклад в изучение природы этого процесса путём создания
различных математических моделей. В большинстве таких моделей износ пути
зависит от числа циклов нагружения и амплитуды вертикальной нагрузки.
Остановимся подробнее на некоторых моделях и рассмотрим их достоинства и
недостатки.
Согласно
экспоненциальной модели (1), показатель относительной осадки, который прямо пропорционален
интервалам между техническими осмотрами состояния пути, зависит от величины
давление на балластный слой. Давление на балластный слой, в свою очередь,
зависит от жёсткости пути.
|
|
(1) |
где ![]() – показатель относительной осадки;
– показатель относительной осадки;
![]() – относительное число циклов нагружения;
– относительное число циклов нагружения;
![]() – общее число циклов нагружения;
– общее число циклов нагружения;
![]() – давление на балластный слой;
– давление на балластный слой;
![]() – давление на балластный слой от
– давление на балластный слой от
относительного числа циклов нагружения;
![]() – показатель степени.
– показатель степени.
Из анализа этой
модели следует, что увеличение жёсткости пути негативно сказывается на
характеристиках пути и способствует его более интенсивной осадки.
Согласно модели ДСМ (3), просадка пути зависит от сил, приходящихся на шпалы. Поскольку эти силы
принимают меньшие значение в местах с меньшей жёсткостью балласта, то
увеличение жёсткости балласта приводит к ускорению развития процесса осадки
пути.
|
|
(2) |
где ![]() – просадка пути после
– просадка пути после ![]() циклов нагружения;
циклов нагружения;
![]() – начальная просадка (функция силы,
– начальная просадка (функция силы,
приходящийся на шпалы);
![]() – поправочный коэффициент.
– поправочный коэффициент.
В модели Сато (3) росадка зависит от коэффициента ![]() , прямо пропорционального давлению,
, прямо пропорционального давлению,
приходящемуся на шпалы и ускорению балласта. Эти оба параметра являются
функцией балластной жёсткости и их значения возрастают по мере увеличения
жёсткости балласта.
|
|
(3) |
где ![]() – просадка
– просадка
пути;
![]() – число циклов нагружения;
– число циклов нагружения;
![]() ,
, ![]() – поправочные коэффициенты;
– поправочные коэффициенты;
![]() – коэффициент, прямо пропорциональный
– коэффициент, прямо пропорциональный
давлению на шпалы.
Подобно модели (3), в модели Хошино (4), показатель ухудшения характеристик пути в вертикальной плоскости прямо
пропорционален фактору строения J, на который влияют величины давление на шпалы
и балластного ускорения
|
|
(4) |
где ![]() – коэффициент ухудшения параметров пути;
– коэффициент ухудшения параметров пути;
![]() – фактор нагрузки;
– фактор нагрузки;
![]() – фактор строения;
– фактор строения;
![]() – фактор состояния.
– фактор состояния.
В модели Герена (5) интенсивность просадки является функцией амплитуды упругой деформации.
Согласно ей, рост деформации приводит к росту просадки пути.
|
|
(5) |
![]() – просадка пути;
– просадка пути;
![]() – число циклов нагружения;
– число циклов нагружения;
![]() – амплитуда упругой деформации во время
– амплитуда упругой деформации во время
циклов нагружения;
![]() ,
,![]() – коэффициенты, зависящие от параметров
– коэффициенты, зависящие от параметров
материала.
Таким образом,
опираясь на модель (5) можно утверждать, что уменьшение жёсткости способствует увеличению
интенсивности развития процесса осадки пути. В модели Фролинга (6) также прослеживается подобная зависимость между жёсткостью пути и
интенсивностью развития просадки пути.
|
|
(6) |
где ![]() – просадка пути;
– просадка пути;
![]() – измеренная жёсткость пути в области шпалы i;
– измеренная жёсткость пути в области шпалы i;
![]() ,
,![]() ,
,![]() – коэффициенты, зависящие от параметров пути;
– коэффициенты, зависящие от параметров пути;
![]() – преобладающая нагрузка от колеса на рельс;
– преобладающая нагрузка от колеса на рельс;
![]() – относительная нагрузка от колеса на рельс;
– относительная нагрузка от колеса на рельс;
![]() – число циклов нагружения;
– число циклов нагружения;
![]() – показатель степени.
– показатель степени.
Подводя итог отметим,
что, согласно моделям (1) – (4) увеличение жёсткости пути негативно влияет на характеристики пути в
вертикальной плоскости путём ускорения деградационных процессов, в то время как
модели (5) – (6)
свидетельствуют об обратном (увеличение жёсткости пути замедляет рост его
просадки). Из этого можно сделать вывод, что не существует единого мнения
насчёт характера зависимости между жёсткостью пути и интенсивностью ухудшение
его характеристик, а задача поиска оптимальных значений жёсткости является
особо актуальной.
Использованные источники
1. Сергеев, И.К. К
вопросу о методиках оценки некоторых динамических параметров подвижного состава
при высокоскоростном движении / И.К. Сергеев, О.Ю. Емельянов, Д.В. Ковин //
Меридиан. – 2020. – №2 – С. 465-467.
2. Сергеев, И.К.
Математическая модель движения вагона с учётом особенностей строения пути, в
кн.: «Современные проблемы железнодорожного транспорта», сборник трудов по
результатам международной интернет-конференции – М.: МИИТ, 2019 – том №1 – С.
274-280.
3. Емельянов, О.Ю.,
Быков А.И. Развитие транспортной системы и экономики путём качественного
преобразования конструкции подвижного состава, в кн.: «Актуальные аспекты и
приоритетные направления развития транспортной отрасли», материалы молодежного
научного форума студентов и аспирантов транспортных вузов с международным
участием – М.:Перо, 2019 – С. 284-287.
References
1. Sergeev, I.K. K
voprosu o metodikah ocenki nekotoryh dinamicheskih parametrov podvizhnogo
sostava pri vysokoskorostnom dvizhenii / I.K. Sergeev, O.Ju. Emeljanov, D.V.
Kovin // Meridian. – 2020. – №2 – p. 465-467.
2. Sergeev, I.K.
Matematicheskaja model’ dvizhenija vagona s uchjotom osobennostej stroenija
puti, v kn.: «Sovremennye problemy zheleznodorozhnogo transporta», sbornik
trudov po rezul’tatam mezhdunarodnoj internet-konferencii – M.: MIIT, 2019 – vol №1 –
p. 274-280.;
3. Emeljanov, O.Ju.,
Bykov A.I. Razvitie transportnoj sistemy i jekonomiki putjom kachestvennogo
preobrazovanija konstrukcii podvizhnogo sostava, v kn.: «Aktual’nye aspekty i
prioritetnye napravlenija razvitija transportnoj otrasli», materialy
molodezhnogo nauchnogo foruma studentov i aspirantov transportnyh vuzov s
mezhdunarodnym uchastiem – M.:Pero, 2019 – p. 284-287.