Конечные
схемы разброса точечных множеств на поверхности антенны солнечного
концентратора могут быть построены для пары параметров (u,v),
заданных в каркасно-кинематическом методе формирования поверхностей (рис.1).
Для
построения таких схем распределения точек зададим кусок поверхности θ, в
декартовой системе координат OXYZ(RM)
евклидова пространства R3[1,
c.23]. Каждая точка Aij
некоторой центральной поверхности несмещенных оценок θ определена двумя
значениями (ui,vj)
как пересечение семейства линий: mi=m(ui);
nj=n(vj).
В
плоскости Σij строится
распределение точечного множества {Aij}.
Расположим его отдельные реализации Aij(k) в
возрастающем порядке относительно граничных точек диапазона [2,c.233]:
Aij(1)<Aij(2)<…<Aij(k)<…<Aij(N).
(1)
Каждой
точечной реализации Aij(k)
ставится
в соответствие некоторая вероятность Pj(i):
Pij(Pij(1),Pij(2),…,Pij(N))
. (2)
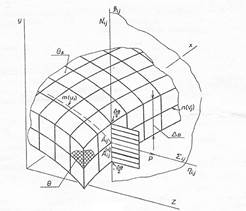
Рис.1.Равновероятное
распределение точечных множеств на
поверхности
концентратора
Предполагается,
что интервал![]() выбран,
выбран,
содержащим все значения точечных множеств с суммарной вероятностью:
![]() = 1.
= 1.
(3)
Совокупность
(1), (2), на основании (3) позволяет получить рабочую схему распределения для
каждой точки поверхности![]() :
:
(Aij)
=  ,
,![]() =1.(4)
=1.(4)
На
основании распределения вероятностей реализаций Aij(k)
в
вероятностном диапазоне [3,c.107],
модель (4) может быть представлена графически (рис.1).
Для
некоторой конечной схемы разброса точечных массивов или соответствующих им геометрических
параметров может быть задана оригинальная функция энтропии в виде:
H(mi)=![]() log(
log(![]() . (5)
. (5)
Эта
функция должна быть определена не только для разброса точечных множеств [4,c.33],
но и на неограниченном распределении:
H(mi)
= –![]() (mi)logf(mi)dmi.
(mi)logf(mi)dmi.
(6)
Для
моделирования удобнее использовать критерий энтропийного значения погрешности:
∆э
= 0,5exp[H(x/y)].
(7)
Энтропийная
погрешность ∆э определяет
эффективный интервал неопределенности 2∆э, включающий лишь ту
часть распределения погрешностей, в которой содержится основное множество
возможных значений случайной погрешности [5,c.74],
при этом какая-то их часть остается за пределами диапазона 2∆э.
Способы
задания геометрических форм элементов солнечных концентраторов [6,c.84]
могут зависеть от различных типов законов распределения, определяющих разброс
случайных реализаций точек поверхности объекта относительно центрированных оценок,
образующих каркас геометрической модели, заданной поверхности Ѳ.
Такую поверхность будем
называть центральной, относительно нее задаются все законы распределения
случайных значений точечных массивов.
Каждая
точка срединной поверхностиѲ[7,c.69]
определена числами (ui,vj),
Aij=f(ui,vj),
представляющими пары реализаций независимых параметров U
и V в каркасно-кинематическом методе
моделирования поверхностей (m=m(u);
n= n(v)).
Относительно характеристикиn (vj)
в точке Aij(k)ϵ
Ѳпостроен
базовый триэдр локальной системы координат (oβijτijηij).
В плоскостиo
βijηij
определен
нормальный закон распределения точечных реализаций Aij=f1(Aij)
на бесконечном интервале.
С
позиций теории погрешностей, неограниченная область определения функции f1(Aij)
должна быть ограничена эффективным интервалом ∆,
который содержит с требуемой вероятностью множество реализаций точечных
массивов.
Наиболее
простой и достоверный метод решения этой задачи связан с вычислением энтропийного
диапазона достоверности, определяющего параметры равновероятного закона f2(Aij)
равноценного заданному f1(Aij)
в плане содержания неопределенности, то есть энтропии. Равномерное
распределение f2(Aij)
имеет фиксированные границы: Amin
–
левую; Amax–
правую, поэтому вопрос выбора доверительной вероятности такого закона не
ставится. С вероятностью P=1
все значения точечных множеств содержатся в интервале:
∆ij
= ∆э
= Amax – Amin
(8)
На
основании принятого допущения о независимости законов распределения
геометрических множеств, энтропия точки поверхности H(Aij)
зависит лишь от значений параметров (ui,vj)
математической модели и не зависит от распределений значений других точек
поверхности солнечного модуля Ѳ.
Величины
параметра приведения kэ
могут быть рассчитаны для любых бесконечных законов, поэтому соотношение (8) представляется
в общем виде:
∆ij
= 2 kэσij,
(9)
где
kэ –
энтропийный коэффициент, с вариациями в диапазоне:
1,1≤
kэ≤2,066 (10)
для
различных законов распределения:
kэ=2,066
– нормального; kэ=1,73
– равномерного; kэ=2,02
– Симпсона;
kэ=1,93
– Лапласа; kэ=1,11
– арксинусоидального.
Энтропийный
подход позволяет увеличить точность моделирования поверхности концентратора [9,c.165]
путем замены текущего интервала погрешностей эффективным энтропийным интервалом
2kэσ в Nраз(N=3/кэ).
(Для нормального закона N=1,46).
Список
литературы
1.Синицын
С.А. Информационно-статистический метод оптимального моделирования гладких
дифференциальных поверхностей при итерационном проектировании технических объектов
на транспорте// монография. Москва: ФГАОУ ВО «Московский университет путей
сообщения». РОАТ. 2017. 103с.
2.Панченко
В.А.. Создание трёхмерных моделей солнечных теплофотоэлектрических модулей в
системе автоматизированного проектирования // Инновации в сельском хозяйстве.
Теоретический и научно-практический журнал, № (2) 27/2018, с. 232 – 238.
3.Панченко
В.А. Моделирование теплофотоэлектрических модулей для энергоснабжения
инфраструктурных объектов // Современные проблемы совершенствования работы железнодорожного
транспорта: межвузовский сборник научных трудов – Москва: Российский
университет транспорта (МИИТ), 2018, с. 100 – 109.
4.Левчук
Т.В., Маслов А.А. Использование имитационного моделирования для анализа
эксплуатационных испытаний программного обеспечения// История и перспективы
развития транспорта на севере России. 2015. №1. С.32-34.
5.Панченко
В.А. Моделирование солнечных теплофотоэлектрических модулей //
Электротехнологии и электрооборудование в АПК, 2019, 2 (35), с. 71 – 77.
6.Левчук
Т.В., Лочканов Д.С., Морозов К.О. Компьютерное и математическое моделирование
экономических и транспортных процессов// История и перспективы развития
транспорта на севере России. 2014. №1. С.82-84.
7.Левчук
Т.В., Втулкин М.Ю. Инновационные технологии на железнодорожном транспорте//
История и перспективы развития транспорта на севере России. 2012. №1. С.68-71.
8.Панченко
В.А. Моделирование солнечных теплофотоэлектрических модулей различной
конструкции // Экологическая, промышленная и энергетическая безопасность – 2019:
сборник статей по материалам международной научно-практической конференции:
“Экологическая, промышленная и энергетическая безопасность – 2019” (23 – 26
сентября 2019 г.) – Севастополь: СевГУ, 2019, с. 1255 – 1259.
9.Sergey
Sinitsyn, Vladimir Panchenko, Valeriy Kharchenko, Pandian Vasant. Optimization
of Parquetting of the Concentrator of Photovoltaic Thermal Module //
Intelligent Computing & Optimization. Advances in Intelligent Systems and
Computing, Volume 1072, 2020, pp. 160 – 169, https://doi.org/10.1007/978-3-030-33585-4_16.

