Суммарную погрешность моделирования кривой будем оценивать произведением[1,c.56]:
![]() =2
=2![]() , (1)
, (1)
Где kΣ– энтропийный коэффициент заданного распределения погрешности;![]() – СКО распределения.
– СКО распределения.
При нормальном распределении всех составляющих геометрических погрешностей [2,c.74] композиция распределений также будет иметь нормальное распределение, а величина энтропийного коэффициента постоянна и равна (![]() =
= ![]() = 2,066) [3,c.82]. Суммарная СКО
= 2,066) [3,c.82]. Суммарная СКО ![]() может быть вычислена как:
может быть вычислена как:
 , (2)
, (2)
где si – СКО компонентов погрешностей.
В частных случаях возможно суммирование двух погрешностей равномерного распределения, при этом суммарный энтропийный коэффициент может быть вычислен с учетом энтропийной погрешности
![]() =
=![]() . (3)
. (3)
по формуле:
![]() , (4)
, (4)
где C=![]() /
/![]() при
при ![]() ≤
≤![]() и C=
и C=![]() /
/![]() при
при ![]() ≤
≤![]() .
.
В системах геометрического моделирования возможны вариации, когда все погрешности распределены нормально, кроме одной, которая имеет равномерное распределение [4,c.86]. В этом случае сначала вычисляются характеристики суммарного распределения для нормальных распределений при постоянном коэффициенте ![]() =2,066, и далее оценивается погрешность суммарного распределения по приближенной формуле:
=2,066, и далее оценивается погрешность суммарного распределения по приближенной формуле:
![]() , (5)
, (5)
где ![]() – суммарная относительная погрешность для всех нормально распределенных погрешностей; sp –СКО равномерно распределенных погрешностей [5,c.191].
– суммарная относительная погрешность для всех нормально распределенных погрешностей; sp –СКО равномерно распределенных погрешностей [5,c.191].
Погрешность моделирования сложных поверхностей на основе компьютеров включает ряд составляющих:
DI – погрешность задания исходной информации точечным базисом;
DИ – погрешность формы обвода, которая определяется объемом и содержанием исходной информации;
Dа – погрешность построения аппроксимирующих функций;
Dp – погрешность дискретного представления модели во внешней памяти компьютера или техническими средствами графики.
1. Погрешность задания точечного базисаDl вносит систематическую составляющую в суммарную погрешность геометрической модели. Такая погрешность уместна во всех задачах геометрического расчета, связанных с применением конкретной модели.
Суммарная погрешность независимых случайных величин [6,c.105] вычисляется по формуле:
 , (6)
, (6)
где N – количество точек базиса исходных данных; si – СКО составляющих; a – коэффициент доверительной вероятности ( для вероятности P=0,95, a=2).
На основании квантильных оценок (6), по методике вычисления погрешностей, могут быть определены: суммарная погрешность СКО, а также энтропийная погрешность:
![]() =
= ![]() / 0,96;
/ 0,96;![]() =
=![]() /2. (7)
/2. (7)
2. Энтропийная погрешность формы поверхности солнечного концентратора, связана с объемом и количественным содержанием исходной информации [7,c.1257] и вычисляется на основании статистической информационной модели [1,c.47]:
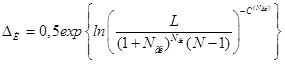 , (8)
, (8)
где L – длина обвода в минимальной матрице; Nгл – порядок гладкости обвода; N – размерность массива узловых точек; ![]() – статистический параметр. На основании вычисленного значения энтропийной погрешности DE (8) вычисляется СКО sИ:
– статистический параметр. На основании вычисленного значения энтропийной погрешности DE (8) вычисляется СКО sИ:
![]() =
= ![]() . (9)
. (9)
3.Среднеквадратическая погрешность суммарного распределения для аппроксимирующих зависимостей рассчитывается по формуле [8,c.69]:
 , (10)
, (10)
В случае малого рассеяния узловых точек при большой протяженности обвода формула упрощается:
![]() , (11)
, (11)
где N – параметр массива узловых точек; L – размерность массива коэффициентов полинома; sD– СКО узловых точек.
СКО узловых точек sD рассчитывается на основании параметра погрешности аппроксимации методом регрессионного анализа.
4. Погрешность представления математической модели с помощью компьютера определяется минимальной метрикой eм предельной дискретизации, заложенной в данном техническом устройстве [9,c.165]. В случае построения графической модели поверхности с помощью чертежного автомата предельная метрика определяется разрешающей способностью устройства.
Параметр дискретизации eм в технических устройствах обычно принимается равным:
![]() = 6
= 6![]() , (12)
, (12)
и энтропийная погрешность реализации математической модели в форме поверхности с помощью компьютеров для нормального распределения несколько ниже:
![]() =
= ![]() . (13)
. (13)
Итак, на основании составляющих СКО вычисляется суммарная погрешность моделирования кривой с помощью компьютеров:
![]() , (14)
, (14)
где составляющие sI,sa,sp, ![]() – определены выше.
– определены выше.
В случае нормального распределения всех составляющих погрешностей суммарная энтропийная погрешность моделирования кривой определяется соотношением:
![]() =0,5
=0,5![]() . (15)
. (15)
Необходимо отметить, что формула (14) при решении типовых задач моделирования может включать какую-то часть составляющие СКО. Так, при моделировании отрезка, ломаной, кривой, заданных точными аналитическими уравнениями, имеет место единственная составляющая погрешности, связанная с дискретным представлением линий техническим средствами (sp).
Список литературы
1.Синицын С.А. Информационно-статистический метод оптимального моделирования гладких дифференциальных поверхностей при итерационном проектировании технических объектов на транспорте// монография. Москва: ФГАОУ ВО «Московский университет путей сообщения». РОАТ. 2017. 103с.
2.Панченко В.А. Моделирование солнечных теплофотоэлектрических модулей // Электротехнологии и электрооборудование в АПК, 2019, 2 (35), с. 71 – 77.
3.Левчук Т.В., Лочканов Д.С., Морозов К.О. Компьютерное и математическое моделирование экономических и транспортных процессов// История и перспективы развития транспорта на севере России. 2014. №1. С.82-84.
4.Левчук Т.В., Казаков М.С., Зверев А.С. Оптимизация систем массового обслуживания// История и перспективы развития транспорта на севере России. 2014. №1. С.84-87.
5.Левчук Т.В., Захаров К.О., Вороненков А.А. Системы управления измерениями// История и перспективы развития транспорта на севере России. 2014. №1. С.190-194.
6.Панченко В.А. Моделирование теплофотоэлектрических модулей для энергоснабжения инфраструктурных объектов // Современные проблемы совершенствования работы железнодорожного транспорта: межвузовский сборник научных трудов – Москва: Российский университет транспорта (МИИТ), 2018, с. 100 – 109.
7.Панченко В.А. Моделирование солнечных теплофотоэлектрических модулей различной конструкции // Экологическая, промышленная и энергетическая безопасность – 2019: сборник статей по материалам международной научно-практической конференции: “Экологическая, промышленная и энергетическая безопасность – 2019” (23 – 26 сентября 2019 г.) – Севастополь: СевГУ, 2019, с. 1255 – 1259.
8.Левчук Т.В., Втулкин М.Ю. Инновационные технологии на железнодорожном транспорте// История и перспективы развития транспорта на севере России. 2012. №1. С.68-71.
9.Sergey Sinitsyn, Vladimir Panchenko, ValeriyKharchenko, PandianVasant. Optimization of Parquetting of the Concentrator of Photovoltaic Thermal Module // Intelligent Computing & Optimization. Advances in Intelligent Systems and Computing, Volume 1072, 2020, pp. 160 – 169, https://doi.org/10.1007/978-3-030-33585-4_16.

