ИНФОРМАЦИОННАЯ МЕТОДИКА ОЦЕНКИ ДОСТОВЕРНОСТИ ПРИНЯТЫХ РЕШЕНИЙ НА ЭТАПАХ РЕШЕНИЯ СИТУАЦИОННОЙ ЗАДАЧИ СУБЪЕКТА

В ситуационных моделях трудно установить функциональные связи между управляющими параметрами входа и характеристиками выхода на любом уровне [1,c.261]. Управляющие параметры нулевого уровня в форме желаний, планов, идей видоизменяются при переходе с уровня на уровень и их количество возрастает. При этом величины доверительных диапазонов новых параметров принятия решений должны уменьшаться (рис.1). Иными словами, при переходе с уровня на уровень результаты принятых решений должны быть получены с определенной точностью по отношению к точности предшествующего уровня[2,c.33].

       В процессе принятия решений по ситуационной модели уровня субъект получает ряд параметров, которые с заданной степенью точности характеризуют его продвижение к судьбоносной цели[3,c.114]. Любая математическая модель, а тем более эвристическая или стохастическая модель, не является абсолютно точной по отношению к реальной ситуации, которую описывает данный блок уровня, а всего лишь в той или иной мере модель адекватна этой ситуации. Поэтому все значения параметров решений принятых на основе модели данного уровня могут рассматриваться как некоторые случайные реализации в своих доверительных диапазонах [4,c.77].

         Перед началом этапа решения ситуационной задачи субъект располагает доверительными диапазонами исходного или нулевого состояния ∆Pr_i⁽⁰⁾ по всем параметрам принятия решений, которые должны быть реализованы в конце этапа решения задачи в диапазонах  ∆Pr_i*[5,c.177]:

                                      ∆Pr₁*,  ∆Pr₂*, … ,  ∆Pr_n*.                                          (1)

 Количество параметров любого этапа всегда меньше общего числа параметров принятия решений глобальной ситуационной задачи [6,c.199]:

                              ∆Pr₁⁽⁰⁾, ∆Pr₂⁽⁰⁾, … , ∆Pr_к⁽⁰⁾,    где    k<n .                            (2)

         Тогда полный прирост количества информации, который должен быть получен в результате выполнения этапа решения ситуационной задачи, определится соотношением:

          Inf(Pr*) = ln∆Pr₁⁽⁰⁾/ ∆Pr₁* + ln∆Pr₂⁽⁰⁾/ ∆Pr₂* +… + ln∆Pr_k⁽⁰⁾/ ∆Pr_k*       (3)

или по свойствам логарифмов:                       

          Inf(Pr*) = ln[(∆Pr₁⁽⁰⁾ ∆Pr₂⁽⁰⁾ …  ∆Pr_к⁽⁰⁾)/( ∆Pr₁^* ∆Pr₂^* …  ∆Pr_к^*)].           (4)

         Характеристика Inf(Pr*) достаточно полно отражает суть процесса принятия решения, подготовленного с помощью математической модели данного уровня. В то же время, количество параметров изменяется при переходе от этапа к этапу, поэтому для удобства сравнения результатов на различных этапах целесообразно определить некоторую усредненную характеристику информации:

                                         Inf*(Pr*) = Inf(Pr*)/k.                                              (5)

         Основная группа доверительных диапазонов промежуточных состояний ситуационной задачи вычисляется в процессе решения этапа и может быть использована повторно другими субъектами, которые решают аналогичные ситуационные задачи с теми же исходными характеристиками Z и случайными факторами ζ:

                                          ∆Pr_i^(j) = f(∆Pr_i^(j-1), Z, ζ).                                           (6)

         Задав исходные доверительные диапазоны, следует скорректировать их границы, после чего можно воспользоваться моделью для пересчета доверительных диапазонов параметров принятия решений в сторону их уменьшения, рис.1.

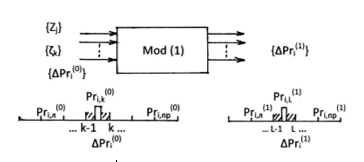
       Рис.1. Схема моделирования этапов решения ситуационной задачи

         Таким образом, решение каждого этапа ситуационной задачи сводится:

1. К назначению закрытого множества параметров принятия решений: {∆Pr_i⁽⁰⁾);
2. Пересчету величин доверительных диапазонов с целью их уменьшения. В этом случае количество информации возрастает, также, как и вероятность правильно принятого решения;
3. Принятию решения по параметрам {∆Pr_i} с целью перехода к следующему этапу решения ситуационной задачи [7, c.199].

При использовании самоформирующихся моделей разброс их характеристик должен быть введен в алгоритм решения задачи.

На вход модели первого уровня, как и моделей последующих уровней. Воздействуют точечные параметры характеристик {Z} и случайных факторов {ζ}, а также параметры принятия решений нулевого или предыдущего уровня {Pr_i}, которые для выполнения вычислений выбираются точечной реализацией из соответствующего доверительного диапазона {∆Pr_i}.

Здесь следует отметить, что выбор точечного значения параметра принятия решения в соответствующем интервале квантования может быть обоснован в двух случаях [8,c.115]:

1.При отсутствии опыта применения модели принимается равновероятная схема распределения на всем доверительном диапазоне и выбор значения параметра производится произвольно.

2.При наличии опыта применения модели появляется дополнительная информация, которая позволяет использовать плотность q(Pr_i^(j)) для сжатия доверительного диапазона.

Далее, в соответствии с алгоритмом, выбирается значение параметра Pr_i,L^(j)в квантильном интервале (L-1,L) доверительного диапазона ∆Pr_i^(j). Здесь также рассматриваются два случая: первый определен равномерным распределением вероятностей; второй – наличием условной вероятностью q(Pr_i,L^(j)/Pr_i,k^(j-1)) и некоторой функцией распределения условной вероятности отличной от равномерного закона.

В любом случае здесь выполняются две процедуры, одна из которых вспомогательная. Суть этой вспомогательной процедуры состоит в том, что конкретные реализации Pr_i,L^(j)дополняют и уточняют функцию условной плотности вероятностей  f(Pr_i,L^(j)/Pr_i,k^(j-1))/

         Таким образом, для условной плотности вычисляется вероятность попадания в интервал (L-1,L) при условии существования исходной реализации предыдущего уровня в интервале (К-1,К) [9,c.62]. Для случая безусловной вероятности уточняется вероятность попадания в интервал (L-1,L) в конце j-го этапа решения ситуационной задачи. Здесь же корректируется обратная зависимость f(Pr_i^(j-1)/Pr_i^(j)).

Список литературы

1.Синицын С.А., Гусарова О.Ф. Информационный подход к разработке и применению иерархических ситуационных моделей интерактивного интеллекта// Москва – МГУ им. М.В.Ломоносова: «Социология» №1, 2019.  с.255-262.

2.Левчук Т.В., Маслов А.А. Использование имитационного моделирования для анализа эксплуатационных испытаний программного обеспечения// История и перспективы развития транспорта на севере России. 2015. №1. С.32-34.

3.Синицын С.А. Информационный подход к разработке методик и алгоритмов типовых ситуационных задач формирования карьеры субъекта// Медицина. Социология. Философия. Прикладные исследования. 2019. №2.  С. 111-117.

4.Левчук Т.В., Ким А.Р. Трехмерное моделирование при визуализации математических и технических задач// История и перспективы развития транспорта на севере России. 2016. №1. С.75-78.

5.Синицын С.А. Формализация погрешностей в задачах оптимизации геометрических моделей// Инновации и инвестиции. 2018. № 11. С. 175-180.

6.Левчук Т.В. Современные пакеты прикладных программ в инженерной и научной деятельности //История и перспективы развитие транспорта на севере России. 2013. №1. С.196-200. 

7.Левчук Т.В., Втулкин М.Ю., Череватый Д.Н. Применение интегрированных пакетов в частных задачах вычислительной математики //История и перспективы развития транспорта на севере России. 2014. №1. С.199-200.

8.Синицын С.А. Информационный подход к разработке методик и алгоритмов типовых ситуационных задач формирования карьеры субъекта// Медицина. Социология. Философия. Прикладные исследования. 2019. №2.  С. 111-117.

9.Левчук Т.В. Эффективность внедрения информационных систем на железнодорожном транспорте//История и перспективы развития транспорта на севере России. 2012. №1. С.60-64.