Рассматривается задача трёхосной ориентации твёрдого тела посредством фильтра Маджвика [1,2]. Процесс реализации поставленной задачи начинается с описания алгоритма работы фильтра в качестве блока инерциальных измерений. БИИ включает в себя трёхосевой гироскоп и трёхосевой акселерометр, отслеживающие поступательные и вращательные движения. Данные с гироскопа и акселерометра преобразовываются в производные кватернионы, описывающие скорость датчика и направление поля тяготения в системе отсчёта Земли относительно системы отсчёта датчика. В целях оптимизации данных, полученных в ходе расчёта и анализа уравнений: оценки, изменении скорости ориентации и целевой функции градиента, применяется один из методов локальной оптимизации — метод градиентного спуска [3]. Во избежание бесконечного множества решений, представленными ориентациями за счёт вращения вокруг магнитного поля или поля гравитации, решение выражается в углах Эйлера [4].
Преобразованный произвольный кватернион угловой скорости имеет вид:
![]()
![]() (1)
(1)
Трёхосевой акселерометр измеряет величину и направление поля тяготения в локальной системе координат.

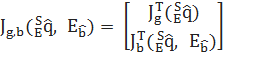
Направление магнитного поля земли измеряется в горизонтальной (уравнения 2-5) и вертикальной осях (уравнения 6-9)
![]() (2)
(2)
![]() (3)
(3)
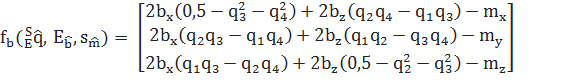 (4)
(4)

![]() (6)
(6)
![]() (7)
(7)
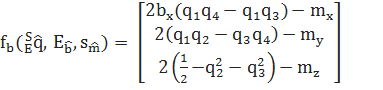 (8)
(8)
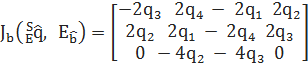 (9)
(9)
Одной итерации достаточно для вычисления приблизительного значения направления в момент t, вычисляемого на основе предыдущей оценки ориентации.
![]() (10)
(10)
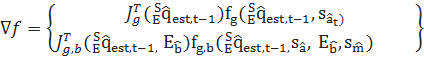 (11)
(11)
Уравнение (12) определяет градиент поверхности решений, определяемой целевой функцией.
![]() (12)
(12)
Из уравнений (13), (14), (15) видно, что фильтр интегрирует расчетную скорость ориентации ![]() , тем самым вычисляет ориентацию
, тем самым вычисляет ориентацию ![]() .
.
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Коэффициент усиления фильтра β представляет все ошибки измерений нуля гироскопа.
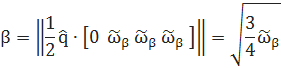
После интегрирования все полученный кватернионы приводятся к нормированному значению, получаем кватернион, описанный в углах Эйлера.
![]()
![]()
![]()
Для того, чтобы определить углы наклона в системе измерения датчика, требуется переход от углов Эйлера в матрицу поворота[4, с.36].
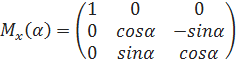 (16)
(16)
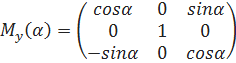 (17)
(17)
 (18)
(18)
После преобразования матриц, получим для осей X,Y,Z:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Углы наклона находим по формулам:

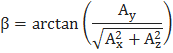
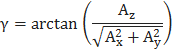
В работе рассмотрен фильтр Маджвика и построен алгоритм его работы над трёхосевой ориентацией тела в пространстве. Вычислены кватернионы силы тяготения и магнитного поля Земли, а так же приблизительного значения направления тяготения, определена целевая функция градиента. Оптимизированы значения вычислений произвольных кватернионов и оценки ориентации, с помощью метода градиентного спуска. Кватернионы приведены к нормированному значению и вычислены в виде углов Эйлера, для дальнейшего удобства их обработки. Просчитаны и определены матрицы поворота и углы наклона тела.
Литература
[1] Sebastian O.H. Madgwick. An efficient orientation filter for
inertial and inertial/magnetic sensor arrays. Report x-io and University of Bristol (UK) vol. 25, 113–118, 30.04.2010
[2] Гордеев В. Н.Кватернионы и бикватернионы с приложениями
в геометрии и механике / Киев: Издательство “Сталь”, 2016 – 316 с. ISBN 978-617-676-099-3
[3] Гасников А.В. Современные численные методы оптимизации.
Метод универсального градиентного спуска М.: МФТИ, 2018.
[4] Журавлев В. Ф. Основы теоретической механики — 2-е
изд. — М.: Физматлит, 2001. С. 23.
References
[1] Sebastian O.H. Madgwick. An efficient orientation filter for inertial and
inertial/magnetic sensor arrays. Report x-io and University of Bristol (UK) vol. 25, 113–118, 30.04.2010
[2] Gordeev V. N. 68 Kvaterniony i bikvaterniony s prilozhenijami v
geometrii i mehanike / V. N. Gordeev. – Kiev: Izdatel’stvo “Stal'”, 2016 – 316 s. ISBN 978-617-676-099-3
[3] Gasnikov A.V. Sovremennye chislennye metody optimizacii.
Metod universal’nogo gradientnogo spuska M.: MFTI, 2018.
[4] Zhuravlev V. F. Osnovy teoreticheskoj mehaniki — 2-e izd. —
M.: Fizmatlit, 2001. S. 23.

