Основным доходом большинства граждан Российской Федерации является заработная плата, жители Липецкой области — не исключение. По данным службы государственной статистики по Липецкой области среднемесячная начисленная заработная плата работников предприятий и организаций Липецкой области в январе-июле 2019 года составляет 33 995 руб. После вычета налога на доходы физических лиц среднестатистический житель Липецкой области получит 29 575 руб.
Допустим, что наш среднестатистический житель Липецкой области взял квартиру стоимостью 2 млн. руб. в ипотеку на 20 лет с первоначальным взносом 600 тыс. руб. При ставке 
, действующая ставка «Сбербанка», ежемесячный платеж составит 13 050 руб.
Помимо ипотеки ему также необходимо оплачивать коммунальные услуги. Пусть он живет один в двухкомнатной квартире, метраж которой составляет около 47 м2. Коммунальные платежи в отопительный сезон составляют примерно 5 200 руб., стоит отметить, что больше половины данной суммы составляет счет за отопление, 2 702 руб.
Следующей статьей расходов является покупка продуктов питания. Согласно данным государственной статистики стоимость минимального набора продуктов питания в Липецкой области в июле этого года составила 3 664 руб. Липецкая область входит в пятерку общероссийских лидеров с наиболее низкой стоимостью продовольственной корзины. Такая низкая стоимость также связана со снижением цен на сезонные продукты, стоимость которых значительно возрастет зимой.
Но будем смотреть правде в глаза, сложно питаться целый месяц на 3 664 руб. И, как мы видим, среднестатистический житель Липецкой области может позволить себе больше… Допустим, что стоимость его продуктовой корзины равна 8 000 руб.
Помимо продуктов питания человеку также необходимы средства личной гигиены. Покупка минимального набора бытовой продукции обойдется около 1 200 руб.
Также не стоит забывать, что время от время человеку необходимо покупать одежду и обувь. В среднем в месяц это выходит около 1 500 руб. Да, одежду и обувь мы покупаем не каждый месяц, но, если мы в январе купим зимнюю куртку и обувь, то получится около 9 000 руб., делим на 6 месяца, допусти, что за полгода человек купил только эти две вещи, в среднем получается 1 500 рублей в месяц.
Таким образом, мы видим, что у среднестатистического гражданина остается 625 руб., которые он хотел бы потратить на свои любимые напитки, чай и кофе. Наша задача — вычислить оптимальную пропорцию чая и кофе для потребителя с учетом его бюджетных ограничений.
В среднем цена кофе составляет 250 руб. за одну пачку, а чая — 70 руб.
Пусть 
— цены на товар 
; Io — бюджет потребителя, а 
— функция потребительской полезности n товаров, которую потребитель хочет максимизировать с учетом своих бюджетных ограничений вида:
,
где сбережения есть один из видов материалов.
Решение подобных задач методом множителей Лагранжа основано на сведении задачи нелинейной оптимизации с ограничениями типа равенств к задаче безусловной оптимизации с новой (расширенной) целевой функцией, называемой функцией Лагранжа вида
,
где переменная 
называется множителем Лагранжа.
Решение данной задачи основано, как известно, на совместном решении системы уравнений
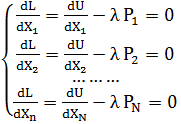(1)
и уравнения
. (2)
Конкретный вид (не только размер, но и структура) матричной системы уравнений зависит от вида функции потребительской полезности 
.
До тех пор, пока неизвестен конкретный вид функции потребительской полезности (и, следовательно, вид частных производных от этой функции) о структуре системы уравнений (1,2) в матричной форме известно не больше, чем это показано в формуле (3), а именно:
. (3)
Интересно сравнить эту неопределенность матричной структуры с определенностью (с точностью до размерности модели) матричной структуры в задаче олигополии.
Итак, целевая функция для нашей задачи равна
,
где 
— количество чая,
— количество кофе.
Пусть функция потребительской полезности чая и кофе, которую потребитель хочет максимизировать, с учетом своих бюджетных ограничений равна
Система уравнений типа (3) примет конкретный вид
,
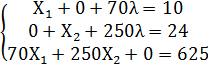или, в матричной форме:
.
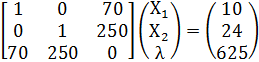Решить данную задачу можно с помощью EXCEL двумя способами: 1) по правилу Крамера с использованием матричных функций 2) с помощью оптимизатора.
На рисунке 1 представлено решение с использованием матричных функций EXCEL. К сожалению, данный метод не всегда является состоятельным, поскольку полученное значения одного неизвестного не связано с другим.
Рисунок 1. Решение с использованием матричных функций
На рисунке 2 представлено решение с помощью оптимизатора EXCEL. Данное решение является корректным.
Рисунок 2. Решение с помощью оптимизатора EXCEL
Таким образом, можно сделать вывод о том, что при решение подобных задач с помощью оптимизатора EXCEL ответ получается более корректным, чем при решении по правилу Крамера с использованием матричных функций.
Список использованных источников
1. Деорнуа, П. Комбинаторная теория игр / П. Деорнуа. — М.: МЦНМО, 2017. — 40 c.
2. Межов И. С. Сравнительная характеристика программно-аппаратных решений для обработки больших данных на российском рынке // Скиф. Вопросы студенческой науки. — август 2019. — №8. — С. 178-181
3. Рязанцева Е. А. Роль обеспеченности доступным интернетом в аспекте цифровизации общества // Материалы XIII международной научно-практической конференции. Под общ. ред. Г.Ф. Графовой, А.Д. Моисеев. Елец, 2019 — С. 367-371
4. Шевченко А. В. Обзор “сквозных” технологий в Российской Федерации // Скиф. Вопросы студенческой науки. — июль 2019. — №7. — С. 149-152
