Гидроциклоны в качестве разделителей, осветлителей, очистителей, классификаторов широко применяются в промышленности благодаря эффекту
центробежных сил. Вопросам теоретического и практического исследования гидроциклонов посвящено множество работ. К их числу относятся
исследования И.П.Плаксина, В.Н.Классена, М.Г.Акопова, А.И.Поварова, А.И.Ангелова, А.И.Жангарина, Р.Н.Шестова, А.М.Мустафаева, Б.М.Гутмана, И.Г.Терновского и др., а также зарубежных исследователей М.Г.Дриссена, Д.А.Дальстрома, Д.Ф.Келсалла, С.Крейгсмана, Г.Кринера, Г.Тарьяна, Г.Ритема и др.[1]. Несмотря на простоту конструкции, кинематика жидкости в нём
сложная, вследствие чего до сих пор нет устоявшейся теории этих аппаратов.
Наиболее применимым и практически исследованным является
цилиндроконический гидроциклон. Менее изученными весьма редко
используемым является гидроциклон с криволинейной формой корпуса, например, овальной. Гидроциклоны простой формы конический, цилиндрический поддаются теоретическому описанию, в то время как в цилиндроконическом нельзя описать одним выражением ломаную линию контура образующей
корпуса, что представляет препятствие для теоретического анализа этих
гидроциклонов. В связи с этим предлагается гидроциклон овальной формы
использовать как аналог цилиндроконического, в связи с чем актуальным является его теоретический анализ.
Движение потока в гидроциклоне трёхмерное, меридиональное движение связано с вращением вокруг оси.
Для решения задачи меридионального течения жидкости внутри гидроциклона достаточно найти функцию тока, удовлетворяющую уравнению Стокса 
(1) и уравнению сплошности (неразрывности) 
(1)
где r, z – цилиндрические координаты; ψ – функция тока.
Искомую функцию тока представим как комбинацию двух функций
(2)
где 
функция тока поступательного равномерного потока : 
a – скорость равномерного потока; 
функция тока гидродинамической
особенности, которую будем искать в виде системы
(3)
где 
переменная, представляющая собой квадрат синуса угла, под которым из начала координат видна рассматриваемая точка с координатами 
и 
неизвестная пока функция от переменной 
.
Подстановка производных от (3) в (1) приводит к дифференциальному
уравнению
(4)
решение которого представим в виде степенного ряда 
где 
…
…
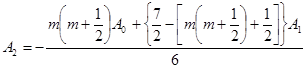Выражение функции тока будет иметь вид:
(5)
где 
коэффициент, определяемый из граничных условий задачи.
Представим 
, где 
– коэффициент, определяющий границу обтекаемой поверхности, получим:
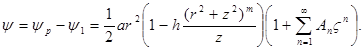(6)
При значениях 
, где 
угол полураствора конуса, и 
получим течение внутри конуса [2].
При 
и 
функция тока описывает течение вокруг и внутри тела овальной формы (рис. 1).
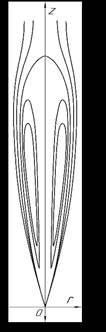
Рис. 1. Линии тока внутри и снаружи овала
Для описания течения внутри гидроциклона с овальной образующей можно воспользоваться циркуляционным потоком внутри контура этого овала.
Значения параметров при этом находятся в пределах: 
При указанных значениях 
ряд в (5,6) быстро сходящийся, что позволяет упростить выражение (6) и представить в виде:
. (7)
Функцию тока гидроциклона с воздушным столбом представим
комбинацией трёх функций
(8)
где 
функция тока равномерного потока при наличии воздушного столба;
(9)
радиус воздушного столба,
функция тока воздушного столба, которую ищем в виде:
(10)
Подстановка производных от (10) в (1) приводит к уравнению
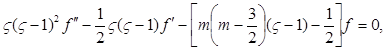(11)
решение которого можно представить степенным рядом 
Здесь 
;
…
… 
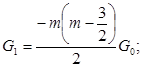
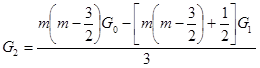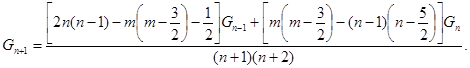
Окончательно:
. (12)
Ряд в (12) знакопеременный, быстросходящийся.
Возвращаясь к уравнению (8) получим:
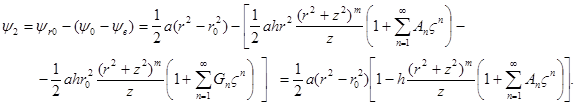(13)
Здесь 
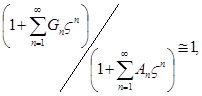
Окончательно:
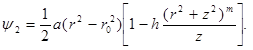(14)
Считается, что диаметр гидроциклона должен быть равен наибольшему
диаметру овала. В этом случае коэффициент 
и показатель 
в формуле (14) определим из следующих условий:
— на границе овала (образующей корпуса гидроциклона) функция тока равна нулю, тогда
(15)
— первая производная от функции тока по 
приравненная нулю, определяет максимальное значение диаметра овала (образующей гидроциклона), откуда
(16)
Задавая желаемые 
и 
получаем требуемые значения и .
Полученная функция тока применима для гидроциклонов с одним верхним сходом, используемых в качестве центробежного фильтра, например, для очистки охлаждающей жидкости в металлорежущих станках, для очистки рабочей жидкости в гидроприводах машин (Трактор Т-180 Брянского
автомобильного завода).
Для представления стока может быть использован точечный сток-источник, описываемый формулами 
или кольцевой сток-источник.
Функцию тока кольцевого стока-источника будем искать в виде системы:
(17)
где 
— радиус окружности кольцевого стока-источника.
Подстановка частных производных от (17) в (1) приводит к
дифференциальному уравнению
(18)
Решение (18) возможно при помощи степенного ряда или переводом его в гипергеометрическое уравнение заменой переменной 
В итоге
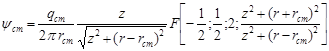, (19)
где qcm — расход стока; 
гипергеометрическая функция; 
.
Выражение функции потенциала кольцевого стока-источника ищем в виде:
(20)
При подстановке частных производных от (20) в уравнение Лапласа (21)
(21)
получаем дифференциальное уравнение
(22)
Решение его возможно при помощи степенного ряда или переводом в
гипергеометрическое уравнение заменой переменной 
, (23)
где 
гипергеометрическая функция.
На рисунке 2 показано совмещение овального гидроциклона с
цилиндроконическим гидроциклоном Келсалла. Для лучшего совмещения конструкций угол конуса гидроциклона Келсалла увеличен с 100 до 120.
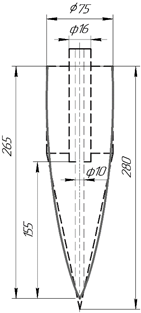
. 2. Совмещение цилиндроконического гидроциклона с овальным
Функция тока для гидроциклона со стоком через кольцевое отверстие будет иметь вид:
. (24)
Здесь 
координата кольцевого сток-источника.
Величину 
можно определить из формулы расхода через верхний сливной патрубок, записанной в следующем виде: 
где 
функция
тока на границе входной кромки верхнего патрубка; 
на границе
воздушного столба гидроциклона. Подставив в (24) координаты окружности входной кромки верхнего сливного патрубка, получим:
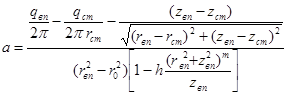. (25)
Радиальные и осевые скорости в гидроциклоне будут определяться по
формулам:
; (26)
. (27)
Составляющие скорости от кольцевого стока здесь определены из
формулы функции потенциала.
Тангенциальную скорость рекомендуется определять по формуле [3]:
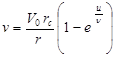, (28)
где 
скорость потока на входе в гидроциклон; 
радиус гидроциклона; 
вязкость потока в стоксах; 
основание натурального логарифма.
Данная формула похожа на формулу диффузии вихря [4], но она
положительно отличается тем, что в ней скорость 
зависит от нескольких
переменных, непосредственно связанных с параметрами конкретного
гидроциклона, влияющих на поведение тангенциальной скорости.
На рисунке 3 приведены линии тока и графики скоростей в овальном
гидроциклоне с параметрами: 
см; 
см; 
7,5 см; 
17 см; 
0,63 см; 
446 см3/с; 
551 см3/с; 
0,5 см; 
0,63 см, 
4,2 см, V0= 500 см/с, 
сст.
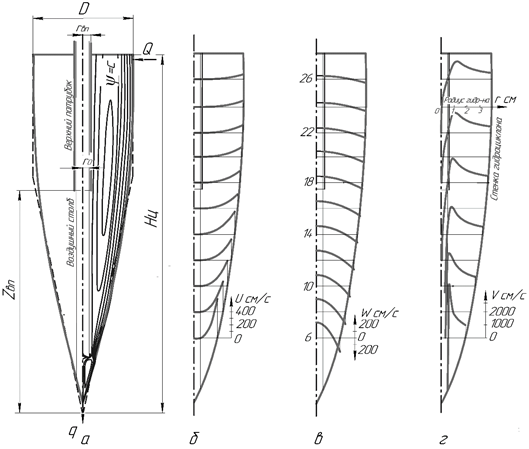
Рис. 3. Кинематика потока жидкости в овальном гидроциклоне
а – линии тока внутри гидроциклона; б – радиальные скорости потока; в – осевые скорости потока; г – тангенциальные скорости потока
Выводы
1. Предложенные формулы для определения скоростей в гидроциклоне повторяют реальный характер их изменения, приводимые в научно-технической литературе.
2. Тангенциальная (окружная) скорость при отсутствии воздушного столба стремится к нулю на оси гидроциклона, при наличии воздушного столба — в зоне воздушного столба и границы цилиндра, ограниченного кольцевым стоком.
3. Тангенциальная скорость внутри зоны воздушного столба меняет знак на обратный входному, что указывает на наличие внутри воздушного столба противоположного вихря, возрастающего при приближении к разгрузочному отверстию. Во внутреннем вихре на оси гидроциклона тангенциальная скорость стремится к бесконечности.
4. Значение тангенциальной скорости на входе в гидроциклон сохраняется постоянным на этом радиусе по всей высоте гидроциклона.
5. Возле нижнего разгрузочного отверстия все скорости возрастают, воспринимая дополнительное воздействие вихревой воронки стока.
Список литературы
1. Терновский И.Г. Гидроциклонирование /И.Г.Терновский. — М.: Наука, 1994. — 352 с.
2. Капустин Р.П. Обтекание потоком жидкости внутренней поверхности конуса // Вестник Брянского государственного университета. 2015. №3(26). С.369-371.
3. Капустин Р.П. Тангенциальная скорость в гидроциклоне // Научно-
технический вестник Брянского государственного университета. 2020. №2. С.337-342. DOI: https://doi.org/10.22281/2413-9920-2020-06-02-337-342.
4. Лойцянский Л.Г. Механика жидкости и газа.- М.: Наука, 1978. 736 с.
List of references
1. Ternovskiy I.G. Gidrotsiklonirovanie. Moscow: Nauka, 1994. 352 p
2. Kapustin R.P. Obtekanie potokom zhidkosti vnutrenney poverkhnosti
konusa//Vestnik Bryanskogo gosudarstvennogo universiteta. 2015. №3(26). P.369-371.
3.Kapustin R.P. Tangencial’naya skorost’ v gidrociklone // Nauchno-tekhnicheskiy vectnik Bryanskogo Gosudarstvennogo universiteta. 2020. №2. P.337-342. DOI. https://doi.org/10.22281/2413-9920-2020-06-02-337-342.
