ЗОЛОТОЕ СЕЧЕНИЕ

«Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора, второе – деления отрезка в крайнем и среднем отношении»

Иоганн Кеплер

Золотое сечение – это некоторое соотношение двух величин, численно равное 1,62 [1]. Среди проблем, связанных с пропорциями предметов пространства, пристальное внимание исследователей в последние годы привлекает вопрос о золотом сечении. Золотое сечение выражает гармонию окружающего пространства. Его можно встретить практически во всех сферах науки и искусства. В связи с широким применением его можно назвать универсальным правилом, которое отражает всю структуру и порядок окружающей среды.

История золотой пропорции начинается еще в VI веке до н. э., его первооткрывателем принято считать Пифагора. Но на самом деле данная пропорция была известна ранее еще во времена построек египетских пирамид и вавилонских храмов.

Затем над сечением трудились такие выдающиеся личности, как Платон, Евклид, Гипсикл, Папп, Луки Пачоли, Леонардо да Винчи, Альбрехт Дюрер, Цейзинг и др. [1].

Леонардо да Винчи (XIV—XV вв.) значительное внимание уделял золотому сечению и его рассмотрение на практике. Он производил сечения объемного тела, образованного правильными пятиугольниками, и обычно получал прямоугольники со сторонами в сопоставлении золотой пропорции. Леонардо дал этой пропорции название золотое сечение, что сохранилось до наших дней.

В последующие века золотая пропорция утратила свое значение в науке. Золотое сечение «открыли» вновь в середине XIX в. В 1855 г. немецкий исследователь-профессор Цейзинг напечатал свой труд «Эстетические исследования». Он обобщил пропорцию золотого сечения и объявил ее универсальной для всех явлений природы и искусства [2].

Пропорция в математике – это равенство двух отношений

Отрезок прямой АВ делится на две части следующими способами:

·две равные части –;

·в любом отношении две неравные части (они пропорций не образуют).

Таким образом, когда. Это и есть золотое деление или деление отрезка в крайнем и среднем отношении (см. рис 1) [3].

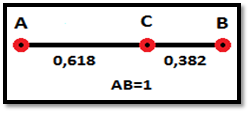
Рисунок 1. Отношение частей отрезка

Переходя к примерам «золотого сечения» в живописной культуре [4], нельзя оставить без внимания деятельность Леонардо да Винчи. Его образ Монны Лизы (Джоконды) до сих пор привлекает внимание исследователей, они обнаружили, что картина основана на золотых треугольниках, которые являются частями правильного звездчатого пятиугольника.

Не обошлась без золотого сечения и такая сфера деятельности, как музыка [4]. Измеряя музыкальное произведение по времени его исполнения, можно выявить золотое деление композиции. В музыке золотое сечение отражает особенности человеческого восприятия временных пропорций и служит ориентиром формообразования (особенно в небольших сочинениях) это и есть точка золотого сечения, здесь и встречается кульминация.

Следует отметить изготовку и роспись различных сосудов [4]. В элегантной форме просто угадываются соотношения золотого сечения (см. рис.2).

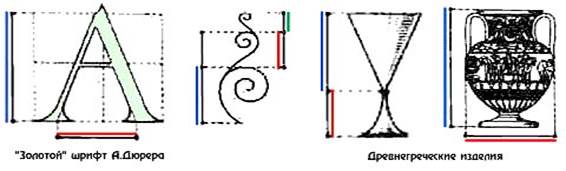
Рисунок 2. Шрифты и предметы

Изучения в области биологии показали, что вирусы, растения, животные и сам организм человека, обладают золотой пропорцией, характеризующей соразмерность и слаженность их строения [5]. Сейчас золотое сечение в обществе признали, как универсальный закон систем живого мира.

Если рассмотреть побег цикория (см. рис. 3), то мы будем наблюдать следующее. От основного стебля образуется отросток. На этом отростке располагается первый листок. Отросток делает сильный выброс в пространство, затем выпускает листок, короче первого, и опять делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньше прежнего и заново выброс.

Рисунок 3. Рост цикория

В животном и растительном мире существует формообразующие тенденции природы. Это симметрия относительно направления роста и движения и золотые пропорции. Природа осуществляет деление согласно этим тенденциям.

Природа не обошла стороной и человека [5]. Выявил пропорцию тела человека Леонардо Да Винчи, он говорил следующее: если фигуру человека перевязать поясом и отмерить потом расстояние от пояса до пят, то эта величина будет относиться к расстоянию от пояса до макушки головы, как весь рост человека относится к длине от пояса до ступней.

В природе и в человеческом теле много пропорций, подчиняющихся золотому сечению. Хотя не все из них повторяют его в точности, но их значение довольно близкое. В любом произведении искусства неравные, но близкие к золотому сечению части дают впечатление развитости форм, их динамики, пропорционального дополнения друг другу.

В ходе работы были проведены исследования на соответствие человека золотому сечению. Для измерения соотношений привлекались курсанты Уральского Института ГПС МЧС России. Использовались: отношение длины лица от макушки головы до подбородка к длине лица от макушки головы до кончика носа, отношение длины ладони от запястья до кончиков пальцев к длине ладони от запястья до кончика большого пальца. Часть результатов соотношений приведена в таблице 1.

Таблица 1.

От места наблюдения в архитектуре и в живописи зависит многое, это также упоминается в книгах о «золотом сечении», поэтому некоторые пропорции, в том числе и золотые, могут выглядеть по-другому. Более спокойно для зрительного образа соотносятся размеры в золотом сечении.

В практическое доказательство под исследование попало здание главного учебного корпуса Уральского Института ГПС МЧС России, расположенное по адресу г. Екатеринбург, ул. Мира, 22. Измерениям подлежали фасад здания (отношение высоты фасада к ширине в условных единицах) и само здание (длина здания к его ширине в условных единицах). Порядок измерений представлен на рисунках 13, 14. Отношения длин здания, представленные в таблице 2, соответствуют пропорциям золотого сечения (1,618).

Таблица 2.

Рисунок 4. Фасад здания УрИ ГПС МЧС России

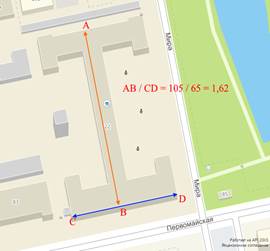
Рисунок 5. Здание института на карте

Изучая золотое сечение в различных сферах было установлено, что данная пропорция универсальна и имеет довольно широкое применение, начиная с математики и заканчивая структурой человека. Проведенные исследования практически доказывают сущность пропорции.

Литература

1.     Н. Васютинский «Золотая пропорция» – М., «Молодая гвардия», 1990

2.     А. Азевич «Двадцать уроков гармонии» – М., «Школа-Пресс», 1998

3.     Свободная энциклопедия – Википедия. Ссылка: https://ru.wikipedia.org/wiki/Золотое_сечение

4.     Золотое сечение в живописи, математике и др. сферах. Ссылка: http://www.abc-people.com/data/leonardov/zolot_sech-txt.html

5.     Золотое сечение. Познавательные статьи. Ссылка: http://log-in.ru/articles/zolotoe-sechenie