Одной из самых объективных тенденций формирования пожарной техники сегодня есть постоянный рост не простой аппаратуры, который связан с увеличением круга тех задач, которые можно решить при возможности одинакового увеличения требований к качеству работы различного рода подсистем. Для того, чтобы аппаратура могла работать правильно и находиться в достаточно высокой готовности ее нужно постоянно, а также своевременно оценивать, причем, оценка должна быть именно на надежность аппаратуры, то есть ее технического состояния с отысканием и резервированием ненадежных или малонадежных элементов в случае их обнаружения.
Более сложные решения, которые имеют отнюдь не простую природу, а также усложнение различного рода функциональных связей в технике более современной вместе с значительным увеличением числа элементов в единице оборудования при малой точности оценки надежности может способствовать росту материальных, а также временных ресурсов, которые тратятся на то, чтобы обеспечить контроль работоспособности и локализацию тех отказов, которые возникли в данный момент, а также организацию ремонта систем, что будет способствовать увеличению времени восстановления техники [2].
Различными аналитическими моделями для того, чтобы получить главные показатели надежности модели теории массового обслуживания. События в данных системах представляют собой различные моменты изменения состояния элементов системы, а потому, модель может описать при помощи Марковского процесса. Аппарат анализа Марковских процессов – уравнения Колмогорова-Чепмена, решение каковых – это самая главная основа расчета выходных параметров системы. Но для различного рода задач, которые касаются оценки надежности более сложной системы технического типа, а также ее компонентов, он способствует трудным многоресурсным моделям, анализ каковых при помощи прямого составления и решения уравнений Колмогорова-Чепмена затруднителен, ввиду этого количество данных уравнений будет увеличиваться вместе с увеличением количества факторов, которые должны учитываться в модели.
Для того, чтобы упростить решение данных систем можно применить редукционный метод. Идея данного метода заключается в том, чтобы анализ более трудной структуре модели можно реализовывать по частям, а именно используя совокупность частично декомпозиционных моделей, или по-другому говоря разбивать сложный граф на множество трудных подграфов, которые не будут зависеть друг от друга с точки зрения обслуживания [7].
К примеру, для того, чтобы определить вероятность пребывания в состоянии Е0-Р00 нужно, в согласии с правилами произведения вероятностей произвести разбитие всевозможных трудных состояний системы на более простые подграфы и заранее провести рассмотрение в каждом полученном подграфе два подмножества состояний системы S00, в каковых устройство будет являться работоспособным, а тогда S10, S20 в каковых устройство будет неработоспособным. Здесь нетрудно увидеть, что из каждого состояния подмножества S00 можно попасть в одно из состояний подмножеств S10, S20 только с интенсивностью λ1 и λ2 тогда, обратно только с интенсивностью μ1 и μ2. На основании этого всего для того чтобы определить вероятность нахождения в состоянии Е0 применяется простой граф, которые будет состоять из двух состояний S00⟶S10 и S00 ⟶S20. В результате перемножения вероятности S00, а также графа S00⟶S10 и S00 ⟶S20 мы можем получить Р00(t) (рисунок 1).
В результате различного рода преобразований в символьном виде, нетрудно убедиться, что полученные решением системы дифференциальных уравнений по стандартной методике, полностью совпадают с такими значениями, которые получаются при помощи решения системы редукционным методом. Значительным преимуществом этого метода является то, что решения можно получить без значительного числа вычислений арифметического типа. Применяя данный метод, имеется возможность найти более точные значения вероятностей даже при значительном числе резервных элементов, ввиду преобразования Лапласа реализуются на простых графах [1].
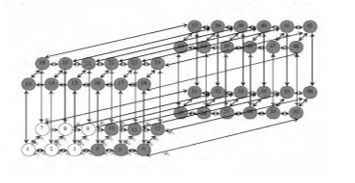
Рисунок 1 – Размеченный граф состояний
Те данные, которые мы получаем при использовании редукционного метода дают точный результат аналитических выражений процесса возникновения отказов и осуществления ремонтов, что дает возможность предсказать часть времени, которое проводится системой в каждом состоянии, на основании чего можно довольно просто произвести оценку надежности всей системы с большой точностью [5].
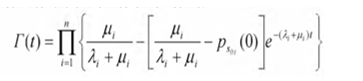
Где:
Г(t) – нестационарный коэффициент готовности;
Ps0i(0) – вероятность нахождения системы устройств в подмножестве состояний s0i в начальный момент времени t=0.
Как видно – редукционное моделирование является очень эффективным методом. Внесем некоторые ясности в использовании данного метода. Вообще, говоря о редукционном моделировании, нужно выделить, в главную очередь, тот факт, что оно обычно используется для того, чтобы получить какие-либо данные о закономерностях взаимодействия элементов в системе для сохранения совокупного структурного образования. Причем, принято считать, что свойства целого образования являются нам известными с основой на законах и теории систем, а сами элементы – это не объекты исследования. При таком методе исследования сами элементы заменятся описанием их внешних свойств. Применение данного метода (редукционного моделирования) дает возможность разрешить задачи по установлению свойств элементов, а также свойств их взаимодействия, и свойств самой структуры системы, для того, чтобы совокупность отвечала самым лучшим образом принципам целого образования с необходимыми свойствами. [3] Такой метод, как правило, часто применяется для того, чтобы найти методы декомпозиции элементов и изменения структуры, придавая системе в целом новые качества. Данный метод также отвечает целям синтеза свойств системы с основой на применении внутреннего потенциала в отношении изменения. Часто данный метод именно называют «редукционным моделированием» или же методом «технологического» моделирования. Практическим результатом применения метода синтеза в редукционном моделировании становится математический алгоритм описания процессов взаимодействия элементов в целом образовании [4].
Таким образом, было установлено, что произведение расчета главных показателей надежности сложной технической системы при применении редукционного метода в отличие от обычных методов, гораздо больше сокращает время вычислений, что дает возможность увеличить оперативность оценки, но также уменьшить и сами требования, которые предъявляются к вычислительной аппаратуре. Такой метод очень эффективно применять в аналогичных данному случаях, но нежелательно использовать в технике, которая эксплуатируется в различных условиях, так как расчеты в данном случае не смогут дать точную оценку надежности, кроме того нужно учитывать человеческий фактор. А так как техника контролируется и управляется в основном людьми, то для оценки надежности системы необходимо учитывать взаимоотношения людей – сторон процессов. Для теоретического рассмотрения этого вопроса, в том числе и для искусственного интеллекта и кибернетики возможно применения теории игр или её элементов [8].
СПИСОК ЛИТЕРАТУРЫ
- Сарымсаков Т.А. Основы теории цепей Маркова. М.: Гостехиздат, 2017. 208 с.
- Баруча Рид А.Т. Элементы теории марковских процессов и их приложения. М.: Наука, 2016. 511 с.
- Зейфман А.И. Об асимптотическом поведении решений прямой системы Колмогорова // Украинский математический журнал. 2015. № 5. С. 621-624.
- Валеев К.Г., Жаутыков О.А. Бесконечные системы дифференциальных уравнений. Алма-Ата: Наука, 2018. 415 с.
- Герасин С.Н. Проблемы стабилизации распределений неоднородных марковских систем. Харьков: ХТУРЭ, 2016. 212 с.
- Зейфман А.И. О равномерной квазиэргодичности и устойчивости неоднородных марковских цепей с непрерывным временем // Проблемы устойчивости стохастических моделей: Труды семинара ВНИИ системных исследований. 2017. С. 45-47.
- Бабенко К.И. Основы численного анализа. М.: Наука, 2017. 744 с.
- Михаэлис В. В. Применение некоторых критериев при выборе оптимальной стратегии в теории игр // Информационные технологии и проблемы математического моделирования сложных систем. 2016. № 15. С. 89–95.
- Белинская С. И., Козыревская А. В., Климова Н. А., Лучников В. А., Михаэлис В. В., Михаэлис С. И., Петрова Л. В., Черепанова А. Л. Методическое и организационное обеспечение научно–исследовательской работы студентов кафедры «Информатика» ИРГУПС // Информационные технологии и проблемы математического моделирования сложных систем. 2009. № 7. С. 154–163.
- Михаэлис С. И. Информационные технологии в системе научно–исследовательской работы студентов вуза // Информационные технологии и проблемы математического моделирования сложных систем. 2011. № 9. С. 149–153.
- Михаэлис С. И. Формирование информационной культуры студентов гуманитарных специальностей // Информатика и образование. 2007. № 5. С. 110–112.
- Sarymsakov T.A. Osnovy teorii cepej Markova. M.: Gostehizdat, 2017. 208 s.
- Barucha Rid A.T. Jelementy teorii markovskih processov i ih prilozhenija. M.: Nauka, 2016. 511 s.
- Zejfman A.I. Ob asimptoticheskom povedenii reshenij prjamoj sistemy Kolmogorova // Ukrainskij matematicheskij zhurnal. 2015. № 5. S. 621-624.
- Valeev K.G., Zhautykov O.A. Beskonechnye sistemy differencial’nyh uravnenij. Alma-Ata: Nauka, 2018. 415 s.
- Gerasin S.N. Problemy stabilizacii raspredelenij neodnorodnyh markovskih sistem. Har’kov: HTURJe, 2016. 212 s.
- Zejfman A.I. O ravnomernoj kvazijergodichnosti i ustojchivosti neodnorodnyh markovskih cepej s nepreryvnym vremenem // Problemy ustojchivosti stohasticheskih modelej: Trudy seminara VNII sistemnyh issledovanij. 2017. S. 45-47.
- Babenko K.I. Osnovy chislennogo analiza. M.: Nauka, 2017. 744 s.
- Mihajelis V. V. Primenenie nekotoryh kriteriev pri vybore optimal’noj strategii v teorii igr // Informacionnye tehnologii i problemy matematicheskogo modelirovanija slozhnyh sistem. 2016. № 15. S. 89–95.
- Belinskaja S. I., Kozyrevskaja A. V., Klimova N. A., Luchnikov V. A., Mihajelis V. V., Mihajelis S. I., Petrova L. V., Cherepanova A. L. Metodicheskoe i organizacionnoe obespechenie nauchno–issledovatel’skoj raboty studentov kafedry «Informatika» IRGUPS // Informacionnye tehnologii i problemy matematicheskogo modelirovanija slozhnyh sistem. 2009. № 7. S. 154–163.
- Mihajelis S. I. Informacionnye tehnologii v sisteme nauchno–issledovatel’skoj raboty studentov vuza // Informacionnye tehnologii i problemy matematicheskogo modelirovanija slozhnyh sistem. 2011. № 9. S. 149–153.
- Mihajelis S. I. Formirovanie informacionnoj kul’tury studentov gumanitarnyh special’nostej // Informatika i obrazovanie. 2007. № 5. S. 110–112.

