Важной особенностью
электромагнитных подвесов с внутренней обратной связью (магниторезонансных подвесов)
является не только обеспечение свободной левитации взвешиваемых тел, но и
способность сравнительно просто формировать точную информацию об их смещениях и
действующих на них силах. В качестве измеряемой силы может быть инерционная
сила, развиваемая взвешиваемым телом при движении основания с ускорением. В
этом случае электромагнитный подвес (ЭМП) становится носителем информации об
ускорении подвижного объекта [1].
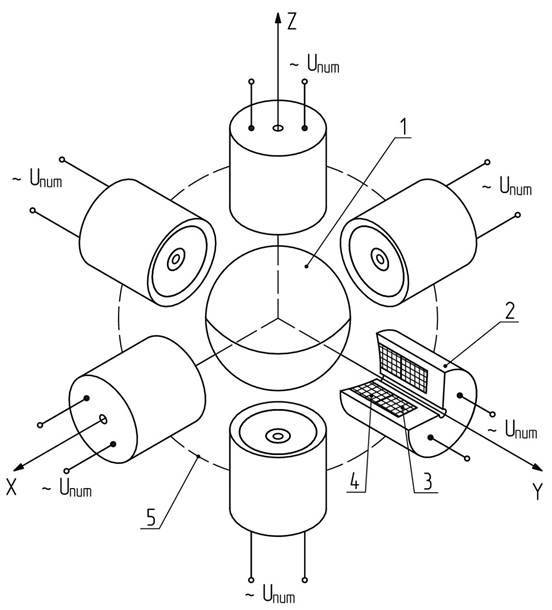
Рисунок
1. Принципиальная схема трехкомпонентного акселерометра на ЭМП с внутренней обратной
связью
Принципиальная схема
трехкомпонентного акселерометра на ЭМП с внутренней обратной связью
представлена на рис. 1. Сферический ротор 1 из магнитопроводящего
материала с высоким удельным электрическим сопротивлением и большой магнитной
проницаемостью (например, феррит 6000НМ) взвешивается в магнитном поле
шестиполюсного статора, имеющего по два полюса на каждый из трех каналов.
Полюсы статора 2 имеют форму броневых сердечников с центральными полюсами, на
каждом из которых размещаются по две обмотки возбуждения 3, 4. Такая
конструкция статоров подвеса позволяет разделить магнитные потоки каждого
полюса и избежать перекрестных связей между каналами. Статоры ЭМП помещаются в
герметичный корпус 5 (показан условно), заполненный вязкой жидкостью. Размеры
ротора и плотность жидкости подбираются таким образом, чтобы взвешиваемый ротор
имел остаточный вес. Заполнение прибора жидкостью необходимо из двух
соображений: во-первых, для увеличения перегрузочной способности и, во-вторых,
для обеспечения демпфирования инерционной массы, что дает возможность упростить
схему резонансного ЭМП, исключив из нее демпфирующие пассивные двухполюсники.
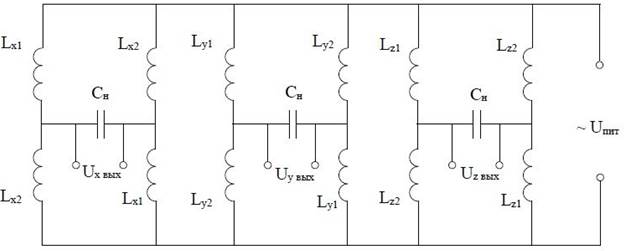
Рисунок
2. Электрическая схема ЭМП трёхкомпонентного акселерометра
Электрическая схема
магниторезонансного подвеса трехкомпонентного акселерометра представлена на
рис. 2. Здесь рабочие обмотки L
противоположных полюсов образуют три электрических моста, в диагонали которых
включены настроечные конденсаторы Cн,
а вся схема питается от источника переменного тока [2].
В качестве выходного
сигнала, характеризующего положение инерционной массы, по каждой из осей
необходимо брать напряжения, снимаемые с соответствующих настроечных
конденсаторов, находящихся в диагоналях мостовой схемы.
При отсутствии ускорений
ротор магнитного подвеса занимает центральное положение и сигналы со всех трех
конденсаторов равны нулю. При наличии ускорения, например, на оси Х на ротор
ЭМП действуют следующие силы: ![]() –
–
инерционная сила, направленная в сторону, противоположную ускорению ![]() ;
;
![]() –
–
выталкивающая сила (сила Архимеда), направленная в сторону действия ускорения ![]() .
.
Если масса ![]() вытесненного
вытесненного
объема жидкости меньше массы ротора ![]() ,
,
то результирующая сила равна
![]()
и направлена в сторону,
противоположную направлению действия ускорения ![]() .
.
Уравнение движения
инерционной массы акселерометра относительно корпуса прибора имеет вид
![]() ,
,
(1)
где m – масса ротора с учетом
присоединенной массы жидкости; ![]() –
–
абсолютное перемещение инерционной массы акселерометра; b
– удельный коэффициент демпфирования; ![]() –
–
электромагнитная сила, создаваемая ЭМП при смещении ротора на величину ![]() под
под
действием ускорения ![]() .
.
Для определения
электромагнитной силы ![]() запишем
запишем
уравнения магнитных и электрических цепей при смещении ротора вдоль оси X
при наличии ускорения ![]() [1].
[1].

(2)
где ![]() ,
,
![]() –
–
магнитные потоки под полюсами; ![]() ,
,
![]() –
–
магнитные сопротивления рабочих зазоров; ![]() –
–
число витков в силовых обмотках; ![]() ,
,
![]() –
–
токи в силовых обмотках статоров, ![]() –
–
активное сопротивление обмотки статора.
При смещении ротора на
величину ![]() магнитные
магнитные
сопротивления ![]() и
и
![]() выражаются
выражаются
следующими зависимостями:
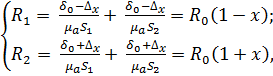
(3)
где ![]() –
–
магнитное сопротивление воздушного зазора одного магнитопровода при центральном
положении ротора; ![]() ,
,
![]() –
–
площадь сечения центрального и периферийного полюсов; ![]() –
–
абсолютная магнитная проницаемость среды, заполняющей зазор ![]() между
между
ротором и статором; ![]() –
–
относительное смещение ротора из центрального положения.
Результирующая
электромагнитная сила, действующая по оси X
при смещении ротора на величину ![]() ,
,
равна
![]()
(4)
Решая уравнение (2)
относительно потоков ![]() и
и
![]() и
и
подставляя полученные выражения в (4), после соответствующих преобразований
получим значение ![]() для
для
установившегося состояния:
![]() ,
,
(5)
где ![]() –
–
электромагнитная сила, развиваемая одним полюсом при центральном положении
ротора; ![]() –
–
добротность силовой обмотки статора;![]() –
–
параметр, характеризующий настройку электрического контура относительно частоты
питающего напряжения ![]() .
.
Таким образом, в
установившемся состоянии уравнение сил, действующих по оси X,
имеет вид:
![]() .
.
(6)
Зависимость выходного
напряжения ![]() от
от
относительного смещения ротора ![]() [3]:
[3]:
![]() .
.
(7)
Для определения
статической характеристики акселерометра ![]() необходимо
необходимо
пренебречь членами, содержащими ![]() и
и
![]() .
.
Тогда из (6) и (7)
получим:
![]() ,
,
(8)
где ![]() –
–
напряжение питания контура; ![]() –
–
начальная жесткость ЭМП при настройке контура на вторую точку половинной
мощности ![]() .
.
Как следует из (8),
уменьшая начальную жесткость ![]() можно
можно
неограниченно увеличивать чувствительность прибора, тем более, что в данном
случае принципиально отсутствует сухое трение. Однако при этом соответственно
уменьшается величина максимального ускорения, измеряемого акселерометром, так
как уменьшается величина максимальной центрирующей силы, которую может развить
ЭМП. Такой подход уместен при разработке акселерометров для измерения малых
ускорений на космических аппаратах.
Принимая силовую
характеристику ЭМП линейной и полагая ![]() ,
,
можно записать:
![]() .
.
Обозначим ![]() ;
;
![]() .
.
Тогда выражение (8) примет вид:
![]() .
.
Практически с помощью
такого акселерометра можно измерить перегрузку ![]() с
с
точностью ![]() .
.
Это ограничение
обусловлено нестабильностью питающего напряжения, наличием нулевого сигнала,
вызванного несимметрией электрических и магнитных цепей, нелинейность
статической характеристики.
Жесткость ЭМП выбирается
из условий обеспечения заданного диапазона измерения ускорений:
![]() ,
,
где ![]() –
–
допустимое смещение ротора ЭМП, обеспечивающее заданную линейность статической
характеристики.
С учетом нелинейностей
статическая характеристика акселерометра, построенная в соответствии с
формулами (5) и (7) представлена на рис. 3.
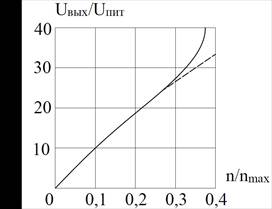
Рисунок
3. Статическая характеристика акселерометра
Анализ мостовой схемы
подвеса позволил получить зависимость выходного напряжения, снимаемого с
диагоналей моста, от относительного смещения ротора и построить статическую
характеристику акселерометра. Показано, что, уменьшая начальную жесткость
подвеса, можно увеличивать чувствительность прибора, однако такой подход
уместен при использовании акселерометра в космическом пространстве.
Список литературы:
1.
Осокин
Ю. А., Герди В. Н., Майков К. А., Станкевич Н. Н. Теория и применение
электромагнитных подвесов. — М.: Машиностроение, 1980.
2.
Герди
В.Н., Крикун В.И., Шахов С.А. Проектирование электромагнитных подвесов
гироприборов и акселерометров с применением ЭВМ: Учеб. пособие ч. I.
М.: МГТУ, 1989.
3.
Герди
В.Н., Крикун В.И., Шахов С.А. Проектирование электромагнитных подвесов
гироприборов и акселерометров с применением ЭВМ: Учеб. пособие ч. II.
М.: МГТУ, 1991.

