- Введение.
Генетический алгоритм представляет собой метод эвристического поиска, основанный на теории естественной эволюции Чарльза Дарвина. Этот алгоритм отражает процесс естественного отбора, где наиболее приспособленные особи выбираются для того, чтобы произвести следующие поколения. Цель алгоритма – найти результат, являющийся или близкий к ответу на поставленный вопрос.
Тема, рассмотренная в данной статье, в настоящее время, является крайне актуальной, ввиду того, что все чаще требуется оптимизировать вычисления и метод нахождения результатов, а также возрастает необходимость в современных быстрых и производительных системах интеллектуального поиска, где также широко применяются генетические алгоритмы. Помимо вышеуказанных проблем, генетические алгоритмы часто используются в различных системах прогнозирования, что позволяет специалистам из различных областей деятельности иметь представление, какие непредвиденный обстоятельства могут случиться в будущем.
На данный момент, уже разобрано множество различных операторов скрещивания, но, в то же время, существует ряд методов, информации по которым крайне недостаточно.
Новое поколение решений/потомков создаётся на основе решений/потомков предыдущего поколения. Базовая стратегия генетического алгоритма заключается в получении наилучшего решения/потомка путём скрещивания родительских генов [1, с. 1].
Одним из этапов генетического алгоритма является фаза скрещивания. Существуют различные подходы к скрещиванию в попытке получить оптимальное решение как можно раньше, при минимальном количестве поколений. Выбор операторов скрещивания оказывает большое влияние на производительность ГА. Операторы делят на 3 категории:
- Стандартные;
- Двоичные;
- Зависящие от области применения;
- Бинарные операторы скрещивания
- Random Respectful Crossover
В данном методе выбор родителей для скрещивания и генерация потомков происходят на основе вектора подобия родителей. Сначала создается вектор подобия акой, что если оба гена родителей равны, то вектор подобия содержит это значение. Иначе, содержит пустое значение.
После формирования вектора подобия, с его помощью создаются два потомка. Если вектор содержит 1, то ген обоих потомков равен 1, иначе 0. Если же вектор подобия содержит пустое значение, дочерний ген выбирается случайным действительным числом. Если это число <0,5, то 1, иначе – 0.
Процесс работы алгоритма представлен на Рис.1. Алгоритм дублирует гены родителей в потомках, в тех местах, где они идентичны.
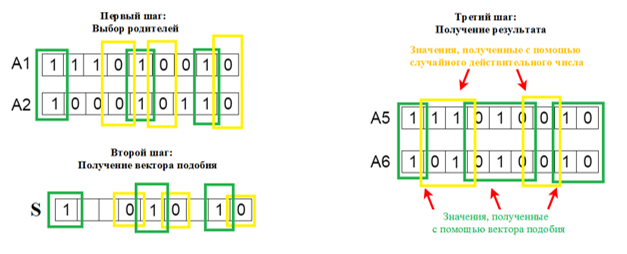
Рис. 1. – Random Respectful Crossover (RRC)
- Masked Crossover
В этом алгоритме используется вектор-маска, чтобы определить, какие гены потомки унаследуют от родителей. Первый шаг – копирование генов родителей. Гены первого родителя дублируются на первого потомка, а второго родителя – на второго потомка. Второй шаг – потомки обмениваются генами, если значение вектора-маски родителя в некоторой позиции равно 1, а значение вектора-маски другого родителя в этой же позиции равно 0.
Вектор-маски задаются случайным образом. На каждой итерации генетического алгоритма вектора-маски наследуется потомством от родителей. Затем вектор-маска потомства, а также родителя, подвергается модификации. Процесс модификации основан на сравнении пригодности потомства и родителей. Если были созданы хорошие потомки, то не требуется менять маски родителей. В ситуации, когда получены плохие потомки, вектор–маски требуется изменить.
- 1 – Bit Adaptation crossover
В этом методе последний бит вектора решения зарезервирован для одного из двух типов примененного оператора скрещивания. «0» соответствует равномерному скрещиванию, а «1» скрещиванию с 2-мя точками. Выбор метода определяется значением последнего бита, если его значение у родителей совпадает. Если совпадений нет, метод выбирается с помощью случайного числа от 0 до 1. Если значение меньше 0,5, то используется равномерное скрещивание, иначе – двухточечное [2, с. 1]. Процесс выбора метода представлен на Рис.2.
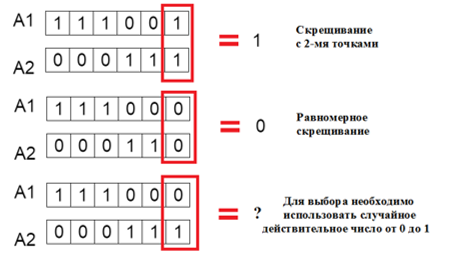
Рис.2. – 1–Bit Adaptation crossover
- Многомерное скрещивание (Multivariate crossover)
Данный метод делит родителя на q подстрок. Принцип основан на выборе случайного значения для каждой подстроки. Если это значение < Pc (некоторая вероятность), то подстрока родителя копируется в строку потомка, иначе применяется одноточечное скрещивание.
Самое принципиальное отличие многомерного скрещивания от других, использующих рекомбинацию от переменной к переменной, состоит в том, что ответ на вопрос «стоит ли переходить» проверяется в многомерном операторе отдельно для каждой подстроки. Что касается других операторов, у них этот вопрос ставится к родителю в целом [3, с. 1].
- Элитарный оператор скрещивания
В стандартном генетическом алгоритме процесс отбора всегда предшествует процессу скрещивания. В этом методе оба процесса интегрированы. На первом шаге, вся популяция случайным образом перемешивается. Затем из каждой последующей пары родительских векторов, с помощью скрещивания, создаются два новых вектора. Из созданной «семьи» выделяются два наилучших вектора, они и станут потомством для следующего поколения.
Применение элитарного отбора традиционным способом, то есть на уровне всей популяции часто может быть причиной преждевременной сходимости алгоритма. Элитарный отбор на уровне семьи исключает эту опасность.
- Гомологическое скрещивание (Homologous crossover)
Этот метод основан на многоточечном скрещивании. Представленная модификация опирается на то, что строки битов определенной длины или имеющие допустимую степень сходства допускаются для участия в скрещивании. Определение степени сходства основано на операторе XOR.
Эта стратегия направлена на передачу строк с указанными параметрами для следующего поколения.
- Count preserving crossover
Данный метод предполагает, что количество бит, равное «1» в каждой хромосоме в начальной популяции P (0) одинаково.
Он гарантирует сохранение постоянного числа битов, равных «1» из-за применения двух списков, отмечая различия между родителями. Список Lup включает в себя позиции те биты, на которых есть различия между родителями, но первый родитель в данной позиции имеет бит, равный «1», а второй равен «0».
Список Ldown аналогично отмечает позиции различий, но первый родитель в данной позиции содержит бит, равный «0», а второй – «1». Процесс создания потомства, который использует эти списки основанный на обмене битами между потомками у тех, позиции, которые обозначены последующими парами элементов из списков Lup и Ldown.
Количество элементов в Lup и Ldown одинаково, что является подтверждением предположения, что количество битов равно «1» является постоянным для всех хромосом в P(0) [4, c. 1].
- Заключение
Существует большое количество различных операторов скрещивания. Каждый из них имеет свои преимущества и недостатки. Большинство из них стремятся решить проблему быстрой сходимости популяции, из-за которой генетический алгоритм может отработать неверно. В данной статье было рассмотрено множество операторов скрещивания, представлены схемы их функционирования, разобраны принципы их работы и случаи, в которых рекомендуется использовать те или иные варианты.
Использованные источники:
- Introduction to Genetic Algorithms [Электронный ресурс]. URL: https://towardsdatascience.com/introduction-to-genetic-algorithms-including-example-code-e396e98d8bf3 (дата обращения 18.03.20).
- 1 – Bit Adaptation crossover [Электронный ресурс]. URL: http://www.tomaszgwiazda.com/onebitAX.htm (дата обращения 18.10.19)
- Multivariate crossover [Электронный ресурс]. URL: http://www.tomaszgwiazda.com/multivarX.htm (дата обращения 18.10.19)
- Основные понятия генетических алгоритмов [Электронный ресурс]. URL: http://www.tomaszgwiazda.com/homoloX.htm (дата обращения 18.10.19)

