ОСОБЕННОСТИ ПОДГОТОВКИ К ОГЭ ПО МОДУЛЮ «ГЕОМЕТРИЯ»

Сегодня важной задачей обучения математике учащихся является подготовка их к государственной итоговой аттестации (ГИА). Первая серьезная проверка ждет учащихся при сдаче Основного государственного экзамена (ОГЭ), минимальный проходной балл которого предусматривает получение 2 баллов за задания из модуля «Геометрия».

Следовательно, подготовка к ОГЭ должна вестись по трем основным направлениям:

• информационная подготовка включает в себя информирование учащихся о структуре экзамена, о правилах и особенностях заполнения экзаменационных бланков; о нормах поведения во время экзамена;
• психологическая подготовка состоит в мотивации учащихся, в создании положительного настроя; в создании установки «Я смогу это сделать» и т.д.;
• предметная подготовка заключается в ознакомлении учащихся с особенностями экзаменационных заданий, обучение умениям решать задания и первой, и второй части ОГЭ.

Следует помнить, что все направления взаимосвязаны. Психологическая подготовка начинается с информирования учащихся об ОГЭ, а наличие мотивации позволит учащимся более внимательно отнестись к предметной подготовке. При этом предметная готовность формирует уверенность в себе и своих силах и невозможна без знаний о структуре экзамена и правилах его проведения.

Задачи из модуля «Геометрия» входят в обе части ОГЭ, т.е.:

• 6 заданий по геометрии требуют численный ответ: ответ представлен числом или последовательностью цифр (задание на выбор верных утверждений);
• 3 задания требуют подробного решения на нахождение численного ответа или приведение доказательства.

Исходя из практического опыта учителей математики и результатов ГИА, можно сделать вывод, что многие учащиеся испытывают сложности при освоении геометрии. Например, Т.Н. Вабищевич, Е.М. Сорочан в своей работе [1] приводят подробный анализ причин возникновений затруднений у учащихся. Помимо этого во время экзамена учащиеся испытывают сильную психологическую нагрузку: в условиях стресса можно растеряться и «все забыть».

Особые трудности возникают у учащихся при решении геометрических задач, что может быть вызвано отсутствием у них интереса, наличие пробелов в знаниях, невозможность выработки алгоритма решения и т.д. Так решение задач геометрическим методом предполагает, по мнению методистов Г.Х. Воистиновой, И.А. Лемедясова [2], умение использовать дополнительные построения, геометрические преобразования, знание свойств фигур, признаки равенства и подобия, различных соотношений в многоугольниках.

Первая часть модуля «Геометрия» состоит из задач, относящихся к основным разделам школьного курса геометрии [3]:

• прямые, углы;
• треугольники, четырехугольники, многоугольники;
• окружность, круг и их элементы;
• площадь геометрических фигур; и т.д.

Во вторую часть модуля «Геометрия» включены три задачи:

• геометрическая задача вычислительного характера, решение которой требует применения различных теоретических знаний из курса геометрии;
• геометрическая задача на доказательство, которое требует применения стандартных приемов доказывания;
• геометрическая задача вычислительного характера, решение которой требует владения различными приемами и способами рассуждений. При решении могут использоваться дополнительные построения и знания (теоремы Чевы и Менелая, свойства высот, биссектрис, медиан и т.д.).

Комплект заданий ОГЭ включает в себя ряд задач, которые не встречаются в большинстве школьных учебников: анализ геометрических высказываний и задания на клетчатом поле. С одной стороны, эти задачи включены в первую часть и, значит, не должны вызывать трудностей у учащихся. С другой стороны, непривычная форма задания увеличивает вероятность допустить ошибку. Поэтому эти задания необходимо регулярно предлагать учащимся, для этого рекомендуется воспользоваться дополнительными материалами (КИМ, сборники задач для подготовки к ОГЭ и пр.), либо разработать их самостоятельно.

Так как большинство тем, предлагаемых на ОГЭ, изучается в 7-8 классах, то и подготовку можно начать в этот период обучения. Предметная подготовка состоит в отработке основных навыков и умений по приведенным темам. Постепенно повышая уровень заданий, необходимо перейти к задачам повышенной сложности и уделить им как можно больше внимания.  Также следует познакомить учащихся с форматом ОГЭ, а для этого необходимо проводить тренировочные работы. Например, при проведении проверочной работы, включить в нее задания из первой и второй части модуля «Геометрия», а также заполнение бланков учащимся. В дальнейшем это позволит правильно распределить силы и время на решение задач ОГЭ.

Первое диагностическое тестирование (проверочная или контрольная работа по геометрии в формате ОГЭ) рекомендуется проводить в начале учебного года. Это позволит оценить уровень знаний учащихся, определить наиболее частые ошибки при выполнении заданий модуля «Геометрия», а также выявить причины этих ошибок. Например, одной из распространенных причин, как выделяет О.Н. Мачина [4], является невнимательность: неправильно прочитали задание, неправильно записали ответ при верном решении, т.е. встречаются ошибки по заполнению экзаменационных бланков.

Поэтому работа по заполнению бланков также должна проводиться систематически, при этом каждый раз следует обращать внимание на правильную запись ответа: в виде целого числа или десятичной дроби, каждая цифра в отдельной клеточке, наименования не пишутся (даже знак градуса). Следует также уделить вниманию написанию запятой: при выборе верных утверждений запятая не пишется; при написании десятичной дроби запятая пишется в отдельной клеточке.

После проработки отдельных вопросов и изучения особенностей ОГЭ проводится повторная диагностика (чаще всего в декабре) по итогам первого триместра. Помимо оценки уровня знаний, это позволит определить степень готовности учащихся к ОГЭ и разработать дальнейшую подготовку с учетом индивидуальных особенностей учащихся. Рассмотрим проверочную работу по геометрии для 9 класса, предложенную авторами статьи.

Проверочная работа по геометрии для 9 класса

Инструкция по выполнению работы [3]

Модуль «Геометрия» содержит 9 заданий: в части 1 – 6 заданий; в части 2 – 3 задания.

Для заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.

Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.

Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки. При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике.

Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения.

Рекомендуем внимательно читать условие и проводить проверку полученного ответа. 

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

После завершения работы проверьте, что ответ на каждое задание в бланках ответов № 1 и № 2 записан под правильным номером.

Вариант № 1

Часть 1

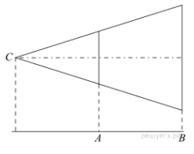
1. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Ответ:
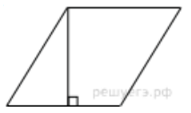
2. Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Ответ:
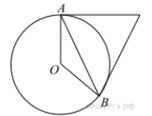
3. Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
Ответ:
4. Найдите площадь параллелограмма, изображённого на рисунке.
Ответ:
5. На клетчатой бумаге с размером клетки 1 см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
Ответ:
6. Какое из следующих утверждений верно? 1) Диагонали параллелограмма равны. 2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. Если утверждений несколько, запишите их номера в порядке возрастания
Ответ:

Часть 2

1. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34.
2. В параллелограмме ABCD проведены перпендикуляры BE и DFк диагонали АС (см. рисунок). Докажите, что ВFDЕ – параллелограмм.
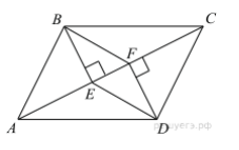
3. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.

В процессе подготовки учащихся к ОГЭ, по мнению Л.Г. Поповой [5], нельзя забывать о взаимодействии с родителями. Во-первых, родители так же, как и учащиеся должны знать особенности проведения экзамена, а также получить рекомендации об организации подготовительной работы. Во-вторых, родители должны быть информированы о результатах тренировочного экзамена. При необходимости должны быть проведены индивидуальные консультации в формате «педагог-учащийся-родитель», это позволит своевременно выстроить работу по преодолению имеющихся проблем изучения геометрии.

В выпускном классе рекомендуется подготовить информационный стенд, на котором будут представлены нормативные документы; бланки и правила их заполнения; веб-ресурсы; рекомендации по подготовке к экзамену и т.д.

Таким образом, можно сделать вывод, что подготовка к экзаменам это ответственный процесс, который включает в себя регулярную, целенаправленную, четко спланированную работу над заданиями. Ученик должен не просто знать теорию и уметь решать задачи, он должен быть уверен в своих силах и быть готов к заданиям ОГЭ. Чем раньше начнется подготовка к экзаменам, тем легче пройдет этот процесс для учащихся.

Список литературы

1. Вабищевич Т.Н., Сорочан Е.М. О некоторых трудностях в изучении геометрии // Социальное партнерство: педагогическая поддержка субъектов образования: сб. матер. Межд. Науч.-практ. Конф. – М.: Пробел-2000, 2018. – С. 335-343.
2. Воистинова Г.Х., Лемедясов И.А. О методах решения планиметрических задач // Аллея науки. – 2018. – Т.3. – №4. – С. 866-872.
3. Кодификатор проверяемых требований к результатам освоения ООПООО и элементов содержания для проведения ОГЭ по математике / ФГБНУ ФИПИ, 2019. – Режим доступа: http://fipi.ru/sites/default/files/document/1573564676/ma_oge_2020_proekt.zip.
4. Мачина О.Н. Эффективные способы подготовки к ОГЭ по математике(раздел геометрии)// Инновационные процессы в физико-математическом и информационно-технологическом образовании: сб. тр. Науч.-пр. конф. –Киров: КОГОАУ ДПО «ИРО Кировской области», 2018. – С. 51-52.
5. Попова Л.Г. Система подготовки к ОГЭ по математике // информационно-коммуникационные технологии в педагогическом образовании. – 2018. – №1. – С. 40-42.

Reference list

1. Vabishhevich T.N., Sorochan E.M. O nekotoryh trudnostjah v izuchenii geometrii // Social’noe partnerstvo: pedagogicheskaja podderzhka sub»ektov obrazovanija: sb. mater. mezhd. nauch.-prakt. konf. – M.: Probel-2000, 2018. – pp. 335-343.
2. Voistinova G.H., Lemedjasov I.A. O metodah reshenija planimetricheskih zadach // Alleja nauki. – 2018. – T.3. – №4. – pp. 866-872.
3. Kodifikator proverjaemyh trebovanij k rezul’tatam osvoenija OOPOOO i jelementov soderzhanija dlja provedenija OGJe po matematike / FGBNU FIPI, 2019. – Rezhim dostupa: http://fipi.ru/sites/default/files/document/1573564676/ma_oge_2020_proekt.zip.
4. Machina O.N. Jeffektivnye sposoby podgotovki k OGJe po matematike(razdel geometrii)// Innovacionnye processy v fiziko-matematicheskom i informacionno-tehnologicheskom obrazovanii: sb. tr. nauch.-pr. konf. –Kirov: KOGOAU DPO «IRO Kirovskoj oblasti», 2018. – pp. 51-52.
5. Popova L.G. Sistema podgotovki k OGJe po matematike // informacionno-kommunikacionnye tehnologii v pedagogicheskom obrazovanii. – 2018. – №1. – pp. 40-42.