ОЦЕНКА ЭКОНОМИЧЕСКОЙ ЭФФЕКТИВНОСТИ ПРОЕКТА С ПОМОЩЬЮ МЕТОДА МОНТЕ-КАРЛО

Введение. Немаловажную роль в оценке экономической эффективности проекта играет анализ рисков для достижения желаемых экономических результатов и увеличения вероятности получения устойчивых экономических выгод от проекта. Управление этими рисками заключается не в минимизации рисков, а в проведении мероприятий для уменьшения вероятности наступления негативных событий и/или последствий от них. Управление рисками — это процессы, которые позволяют заблаговременно принять решения по контролю событий, связанных с риском, оптимизируя успех путем минимизации угроз и максимизации возможностей. Процесс управления рисками проекта обычно включает выполнение следующих процедур:

1. Планирование управления рисками.
2. Идентификация рисков.
3. Качественная оценка рисков.
4. Количественная оценка.
5. Планирование реагирования на риски.
6. Мониторинг и контроль рисков.

На сегодняшний день существует множество методов оценки рисков проекта. Различают качественные и количественные методы. Качественная оценка рисков — это процесс оценки характеристик риска отдельных проектов — вероятности возникновения и воздействия, которые они будут иметь в проекте в случае их возникновения. Этапы качественного анализа рисков:

• идентификация рисков;
• оценка рисков, с использованием рангов воздействия и вероятности;
• расстановка приоритетов между рисками;
• интерпретация результатов.

Задача количественного анализа рисков — числовая оценка общего влияния риска на цели проекта, такие как затраты и график. Результаты дают представление о вероятности успеха проекта и используются для разработки резервов на случай непредвиденных обстоятельств. Методы количественной оценки рисков:

• трехточечная оценка — метод, который использует оптимистические, наиболее вероятные и пессимистические значения для определения наилучшей оценки.
• анализ дерева решений — диаграмма, которая показывает последствия выбора той или иной альтернативы.
• ожидаемая денежная стоимость (EMV) — метод, используемый для определения непредвиденных резервов для бюджета и графика проекта.
• анализ Монте-Карло — метод, который использует оптимистичные, наиболее вероятные и пессимистичные оценки для определения общей стоимости проекта и сроков завершения проекта.
• анализ чувствительности — метод, используемый для определения того, какие риски оказывают наибольшее влияние на проект [1].

Метод Монте-Карло является мощным количественным инструментом, применяемом часто при анализе рисков. Данный метод успешно применяется в компьютерном моделирование [2]. Расчет параметров вероятностных распределений при анализе рисков проекта позволяет должностному лицу, принимающему решение, количественно оценить уровень риска, который возникает при принятии конкретного решения, и, в результате, выбрать решение, обеспечивающее наилучший баланс между выгодой и риском.

Анализ рисков по методу Монте-Карло включает в себя создание математической модели и запуск симуляций с использованием этой модели для оценки влияния рисков проекта. Этот метод помогает в прогнозировании вероятного исхода события и тем самым помогает в принятии обоснованных проектных решений.

Последовательность шагов при анализе рисков методом Монте-Карло:

1. Определение ключевых переменных риска проекта.
2. Определение диапазона пределов для переменных проекта.
3. Указание весовых коэффициентов вероятности для диапазона значений.
4. Установление отношений для коррелированных переменных.
5. Выполнение прогонов моделирования на основе идентифицированных переменных и корреляций.

При проведении расчетов по методу Монте-Карло предполагается, что известны значения всех параметров, например, при расчете рисков инвестиционного проекта необходимо знать такие величины, как ставка дисконтирования, условно-постоянные затраты, амортизация, ставка налога на прибыль, остаточная стоимость, объем инвестиций, срок реализации проекта, количество значений в одной реализации, а также цена, объём выпуска, условно- переменные расходы на единицу продукции (табл. 1,2).

Таблица 1

Исходные данные для моделирования NPV

Таблица 2

Исходные данные для моделирования NPV

При анализе результатов и оценки рисков проекта определяются значения показателей, характеризующих параметры полученного распределения чистого дисконтированного дохода (NPV). Если в качестве критерия оценки инвестиции используется NPV, то к их числу можно отнести:

• наибольшее и наименьшее значения NPV;
• выборочная средняя и среднеквадратическое отклонение NPV.

Используя полученные конкретные распределения значений NPV и ставки внутреннего процента, можно определить основные характеристики риска проекта (табл. 3).

Таблица 3

Характеристики NPV, вычисленные при n=10000

Согласно правилу финансового менеджмента: «Если чистый дисконтированный доход больше нуля, то инвестиционный проект следует принимать к реализации, если чистый дисконтированный доход меньше нуля, то проект подлежит отклонению» [3, 4]. Формула (1) для расчета риска по методу Монте-Карло:

                                                      (1)

где k- количество реализаций, n- количество значений в одной реализации.

На основе метода Монте-Карло получаем, что в тысяче случайных реализаций среднее число отрицательных значений чистого дисконтированного дохода NPV равно 174.59, то есть риск равен 1.7459%.

Для моделирования методом Монте-Карло разработаны различные инструментальные программные обеспечения, один из них Crystal Ball.

В процессе эксплуатации резервуаров возникают технологические и эксплуатационные дефекты, а также развиваются коррозионные процессы в области механических повреждений, что приводит к росту в размерах дефектов, которые могут в дальнейшем стать сквозной трещиной. Также, как известно, что с течением времени вероятность разрушения резервуара увеличивается [5].

Согласно данным Федеральной службы по атомному, технологическому и экологическому надзору число чрезвычайной ситуации растет и последствия от подобных событий все ухудшаются. Например, за период с 2016 по 2019 случилось 210 опасных события.

Рассмотрим пример расчета риска нежелательного события с помощью моделирования методом Монте-Карло в Crystal Ball.

Итак, риск нежелательного события (аварии, инцидента) рассчитывается по формуле:

R = P ∙ V,

где Р – вероятность или показатель частоты нежелательного события, V– ущерб от последствий аварии, инцидента.

Для того чтобы провести вычисления необходимо определить исходные данные, а именно вероятность или показатель частоты нежелательного события и ущерб от последствий аварии, инцидента. За показатель частоты инцидента возьмем данные Федеральной службы по атомному, технологическому и экологическому надзору – 210 опасных случая, а оценка экономического ущерба при возникновении чрезвычайной ситуации будет определяться суммой следующих переменных: прямой ущерб от аварии; затраты на локализацию (ликвидацию последствий) и расследование причин аварии; экологический ущерб; косвенный ущерб; социально-экономические потери (табл.4).

Таблица 4

Исходные данные для моделирования в Crystal Ball

Алгоритм моделирования расчета риска нежелательного события в Crystal Ball:

1. В среде Excel заполнить исходные данные (переменные моделирования, их среднее значение и стандартное отклонение);
2. В окне Crystal Ball щелкнут кнопку «Определение допущения» для каждого среднего значения, последовательно вставая курсором в соответствующие ячейки выбрать вид и параметры распределения (для нашего случая — нормальное).
3. Также в окне Crystal Ball выбрать ячейку, содержащую формулу расчета риска, и щелкнут кнопку «Определение прогноза», количество итераций выбрать 10000;
4. Результаты моделирования программа выведет в графическом виде (рис 1).

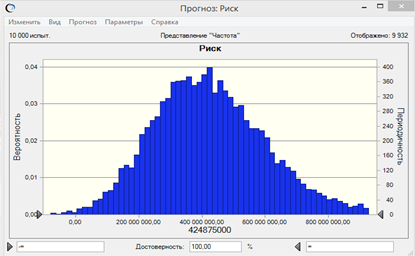
Рисунок 1. Результаты моделирования методом Монте-Карло расчета риска нежелательного события в Crystal Ball

Выводы. Оценка экономической эффективности проекта с помощью метода Монте-Карло является проверенным методом анализа рисков, обеспечивающим целесообразность всех расчетов, простоту восприятия и оценки результатов анализа проекта всеми участниками процесса, однако требует значительных вычислительных ресурсов на расчеты, связанные с большим объемом числовых данных, тем самым, добавляя еще большую ценность этому методу.

Применение числовых данных, собранных путем запуска нескольких симуляций, помогает устранить любые отклонения от проекта в отношении выбора альтернатив при планировании рисков.

Таким образом, риск инвестиционного проекта по методу Монте-Карло рассчитывается, как отношение количества отрицательных значений чистого дисконтированного дохода к общему количеству значений в одной реализации.

Использованные источники:

1. РД 03-418-01. Методические указания по проведению анализа риска опасных производственных объектов. Москва: Закрытое акционерное общество «Научно-технический центр исследований проблем промышленной безопасности», 2010. — 40 с.
2. Решение задач теории вероятностей и математической статистики в среде Scilab: учебно-методическое пособие / А. Н. Титов, Р. Ф. Тазиева. — Казань: КНИТУ, 2019. -120 с.
3. Теплова, Т. В. Финансовый менеджмент: управление капиталом и инвестициями. –Москва: ГУ ВШЭ, 2000. –504 с.
4. Имитационное стохастическое моделирование чистого дисконтированного дохода и риска инвестиционного проекта / Титов А.Н, Тазиева Р.Ф, Фадеева Е.П. // Вестник технологического университета. –Казань, 2017. –Т. 20. –№ 19. –С. 88-92.
5. Особенности коррозионного исчерпания ресурса резервуаров и оценка интенсивности возрастания напряженного состояния в сварных швах / Г.С. Аммосов, Дж.С. Иванов, А.П. Аммосов // Наука и образование. — Якутск, 2017. — №1. – С. 75-80.