Профессиональные опасности
формируются из наличия опасности вредного воздействия химических и
биологических факторов, травмирования и т.д.
При идентификации опасностей
необходимо учитывать все случаи непредвиденных ситуаций, связанных например, с
положением тела при работе, умственной и физической усталость, взаимодействием
работника с оборудованием.
Задачи, решаемые
системой контроля, представлены на рисунке
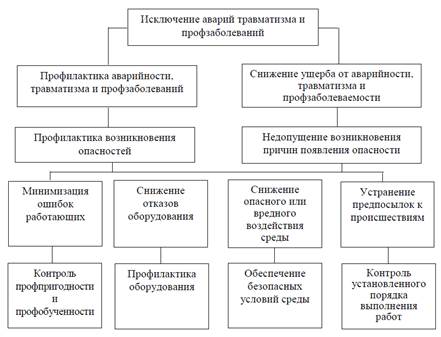
Рисунок – Основные задачи системы контроля
за состоянием безопасности производства
Улучшения контрольно-профилактических
работ делятся на следующие направления:
1. Обоснование объема выборки периодически проверяемых
производственных объектов;
2. Разработка графиков работы органов контроля;
3. Оценка эффективности мероприятий, которые разработаны
по результатам проверок для предупреждения происшествий и профессиональных болезней.
Оптимизация идентификации опасностей
осуществляется за счёт повышения эффективности действий контролирующих органов,
которая состоит в планировании этой деятельности и оптимизации численности
органов контроля.
Обоснование объема и состава
инспектируемых объектов обусловлено невозможностью систематически и качественно
проверять одновременно все производственные объекты, т.к. может быть не
выдержано требование к оперативности управления безопасностью. Для повышения
эффективности контрольно-профилактической работы в этих условиях приходится
проводить выборочный контроль лишь некоторых из них.
Обоснование выборки обследуемых объектов
наиболее целесообразно осуществлять при использовании в качестве критерия
оптимизации информацию о происшествиях и предпосылок к ним.
В первую очередь необходимо планировать те
объекты, где возможно максимальное число происшествий или могут иметь место
наиболее тяжелые последствия от них. Ограничением к объему выборки
запланированных для обследования объектов служат трудозатраты.
Задача оптимизации идентификации
опасностей принадлежит к классу задач линейного (комбинаторного)
программирования.
Способом её решения может служить алгоритм
Колесара, основанный на методе ветвей и границ.
Качество контроля характеризуется вероятностными
параметрами осуществляемых преобразований.
При этом, под вероятностными 
подразумеваются
ошибки первого и второго рода –
; их дополнения до единицы 
; условные вероятности устранения
обнаруженных предположений –
, а под ресурсами –
, необходимыми для
операционного контроля и устранения обнаруженных отклонений, — затраты 
соответственно.
Организация контроля безопасности проведения
конкретного процесса в рассматриваемых условиях может состоять в определении
значений некоторой величины i x , указывающих на необходимость ≠0 и
кратность ( i m =1,2, , K ) осуществления
контроля за каждой отдельной операцией, а задача его совершенствования – в
выборе оптимального (в определенном смысле) 43 вектора X=(
). В качестве
критерия оптимальности и ограничений должна использоваться организационная характеристика
или еѐ
компоненты.
Для уточнения содержания вектора 
необходимо учитывать, что цель
обеспечения безопасности заключается в удержании в допустимых пределах или
минимизации суммарных издержек, либо их одной компоненты – ущерба от
происшествий и профессиональных заболеваний 
и математические
ожидания величин ущерба –
или затрат –
с ними связанных).
Цель совершенствования безопасности проводимых работ
состоит в выборе кратности контроля. Математически это сводится к нахождению m-мерного
вектора кратности контроля X=() , реализующего
одно из двух условий:
где 
– максимально допустимое значение
затрат, необходимое для выполнения контролирующей деятельности; 
– минимальная вероятность
обнаружения опасностей в процессе контролирующей деятельности; P (X) –
вероятность идентификации опасностей при проведении контролирующей
деятельности; S (X)– затраты
на выполнение контролирующей деятельности и устранение выявленных отклонений.
При принятых предположениях вероятность будет
определяться произведением, а затраты – суммой входящих в них частных
показателей процесса:
где 
– вероятность выполнения i — тых
технологических операций без происшествий и предпосылок к ним в течение
определенного времени;
– затраты, необходимые для
организации в это же время контроля безопасности проводимых работ и устранения
выявленных отклонений, i m =1,2,…, .
При условии пренебрежения ошибками первого рода при
контроле
а соответствующие этим организационным процедурам и
допущениям затраты определяются такими соотношениями:
где bk = [1 – Qk(τ)] k 11 + Qk (τ) k 10 –
параметр качества системы контроля;
– условные вероятности устранения
выявленных внештатных ситуаций на i-ом его шаге;
– затраты на организацию контроля и
устранения возникающих на его i-ом шаге предпосылок к происшествиям.
Следующим шагом оптимизации контроля является
определение численности работающих в контролирующих органах.
Ограничения будут определяться исходя из предполагаемой
эффективности контроля и устранения возможных отклонений, сравнения с
эффективностью технических и технологических средств защиты.
Значение 
может задаваться также на основе
статистических соотношений между числом аварий и несчастных случаев и причинами
их возникновения [35]. В качестве одного из возможных методов решения
предложенных задач оптимизации целесообразно использовать градиентный метод
отыскания экстремума:
.
Для решения задач оптимизации могут быть
применены известные алгоритмы и соответствующие им программы. Обоснования
состава и численности персонала органов контроля (ОК) осуществляется в два
этапа: — анализ существующей системы контроля; — синтез системы контроля,
заключающийся в обосновании рациональной численности органов контроля.
Первый этап носит предварительный
характер. Главная цель его проведения состоит в получении качественной оценки
степени дублирования ОК выполняемых ими функций. Решение этой задачи
осуществляется с использованием методики, основанной на расчете параметров,
определяющих взаимосвязь ОК по выполняемым ими функциям.
Исходными данными являются перечень
функций и состав ОК. На основе экспертных оценок (эксперты – руководители
соответствующих ОК) определяется факт участия соответствующего ОК в выполнении
им той или иной функции.
Далее формируется таблица, элементы
которой характеризуют корреляцию между различными ОК по выполнению одинаковых
функций
Оценка структуры ОК и степени дублирования
выполняемых ими функций производится по соответствующему множеству качественных
показателей. Второй этап является основным. Для решения задачи обоснования
рациональной численности ОК разработана методика, сущность которой заключается
в следующем. Рациональное штатное расписание определяется использованием
комплексного критерия 
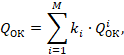
где 
– функции выполняемые i-ым ОК;
– коэффициент, оценивающий его
деятельность;
М – число контролирующих органов
Оценка деятельности каждого органа управления характеризуется
выражением:
где 
– фактическая численность i-ого ОК
– численность i-ого ОК в
случае оптимизации.
Величины коэффициентов 
определяются экспертным путем.
Находится вектор
, который представляет собой
искомые коэффициенты важности функций ОК.
Для обоснования коэффициентов важности ОК использован
метод анализа иерархий, и на основе попарного сравнения важности функций (с
использованием предложенной критериальной шкалы) экспертами осуществляется
оценка важности каждой функции.
Далее с использованием лексического анализа содержания
функций системы контроля в целом и частных функций ОК осуществляется оценка
степени участия ОК в выполнении всей совокупности функций возлагаемых на
систему.
Результаты оценки вклада каждого ОК формируются в
матрицу
Таблица — Оценка вклада каждого органа
контроля в систему
идентификации опасности
|
№ п/п |
Наименование ОК |
Функции ОК |
||||||
|
|
1 |
2 |
… |
j |
… |
… |
L |
|
|
1 |
|
|
|
… |
|
… |
… |
|
|
2 |
|
|
|
… |
|
… |
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
|
i |
|
|
|
… |
|
… |
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
|
M |
|
|
|
… |
|
… |
… |
|
Результаты оценки вклада каждого ОК с учётом важности
компонент вектора
формируются в матрицу 
Матрица R представлена в таблице 2.2.
Таблица — Итоговая матрица R
|
№ п/п |
Наименование ОК |
Функции ОК |
||||||
|
|
1 |
2 |
… |
j |
… |
… |
L |
|
|
1 |
|
|
|
… |
|
… |
… |
|
|
2 |
|
|
|
… |
|
… |
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
|
i |
|
|
|
… |
|
… |
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
|
M |
|
|
|
… |
|
… |
… |
|
Расчет оптимального состава i-ого ОК 
выполняется с использованием
данных, содержащихся в таблице, для каждого i-ого ОК
Таблица — Данные для расчета оптимального
состава органа контроля
|
№ п/п |
Функция ОК |
Интенсивность возниконовения функции |
Длительность выполнения функции |
Количество персонала, задействованного на выполнение |
|
1 |
|
|
|
|
|
… |
|
|
|
|
|
j |
|
|
|
|
|
… |
|
|
|
|
|
L |
|
|
|
|
Необходимые годовые трудозатраты i-ого ОК определяются
следующим образом:
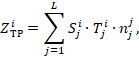
где 
i – интенсивность возникновения j-ой
функции i-ым ОК;
– длительность выполнения j-ой
функции i-ым ОК;
i – количество персонала i-ого ОК;
L – число
функций i-ого ОК.
Оптимальное количество персонала i-ого ОК будет:
N 
=
– нормативный уровень трудозатрат.
Критерием эффективности является степень выполнения
функций если:
– выполнено;
– выполнено недостаточно полно;
– выполнено не полностью;
– не выполнено.
В случае несоответствия значения интегрального
показателя предъявляемым требованиям необходимо приступить к изменению исходных
данных и повторному проведению расчетов.
Процесс повторяется до тех пор, пока значения
интегрального показателя не будут удовлетворять предъявляемым требованиям, но
уже за счет увеличения штатной численности ОК или нормативных трудозатрат, а
также внедрения средств и комплексов автоматизации контрольной деятельности.
Критерий эффективности функционирования системы
определяется по результатам контроля.
Эффективность системы контроля оценивается критерием 
где 
– количество
проверок, которые требуют немедленного принятия решения;
– количество проверок, которые
требуют принятия решения в течение полугода;
– количество проверок, которые
требуют принятия решения в течение года;
количество проверок, которые
требуют принятия решения планово в течение трех лет;
n – общее
количество проверок.
При сравнении полученного значения с фиксированным
значением за прошлый год 
оценивают
эффективность системы контроля.
Однако даже один из выявленных проверкой недостаток
может привести к несчастному случаю.
С целью учета этого фактора используется критерий
комбинации:
где 
– выявленный недостаток;
– заданная постоянная, которая
оценивает дисперсию D(K) по
отношению к K„т .
С целью учета эффективности контроля по отношению к
прошлому году критерий модифицирования запишется следующим образом:
Где
Мероприятия по устранению рисков
могут носить тактический и стратегический характер. В первом случае их выбор
осуществляется при поддержке принятия решений, а финансовые затраты обычно
укладываются в рамки предусмотренных законодательством отчислений.
Во-втором, например, происходит
техническое перевооружение предприятия, которое требует больших финансовых
затрат. В этом случае очень важно определить очередность проведения
мероприятий, т.е. осуществить стратегическое планирование с учетом
осуществления необходимых расходов. Такое планирование происходит при частичном
или полном отсутствии информации, т.е. степень неопределенности очень высока. С
этой целью достаточно эффективна методика, основанная на применении вероятность
статистических критериев, позволяющая накладывать ограничения на финансовые
затраты и время.
Пример применения вероятных
стратегий действий по минимизации рисков приведен на рисунке 4.7. С текущего
момента времени 1 до момента 5 может быть использовано любое из четырех решений
каждое из которых соответствует
стратегиям 
Количественная оценка риска в
каждом из случаев осуществляется экспертным путем в соответствии с
разработанной методикой (глава 3). При стратегии 
риск достигнет величины 
при 93 условиях внешней и
внутренней среды. Если ситуация благоприятна для стратегии 
, а выбрана C1, то
уровень риска вырастает.
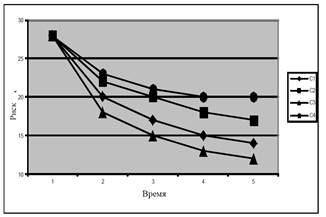
Рисунок – Различные стратегии минимизации
рисков
Если оценочный функционал 
[20, 86]
представить в форме матрицы, элементами 
которой являются количественные
оценки 
а внешняя и внутренняя
характеризуется состоянием q
j , то
матрица будет выглядеть следующим образом:
где 
– совокупность множеств решений по
выбору стратегии 
– характеристики состояний внешней
и внутренней сред; 
– балльные оценки
риска при выборе стратегии k при условии состояния сред j.
Если есть возможность оценить
распределение вероятностей 
на массиве состояний 
заданными
множествами
и 
, эффективность стратегии
определяется с использованием критерия Байеса. В этом случае формулы априорных
вероятностей преобразуются в апостериорные. Эффективным является решение 
при
котором минимум математического ожидания является наименьшим из возможных:
где B – байесовое значение при решении 
При наихудших условиях необходимо
выбирать стратегию с минимальными потерями. В этом случае для оценки стратегии
применяется критерий Вальда. Решение 
должно удовлетворять условию
При точечных измерениях состояний
внешней и внутренней сред используются оценки Фишборна. При отношении вида 
, 
оценки Фишборна 
априорных вероятностей 
представляют собой убывающую
арифметическую прогрессию
Для отношения 
оценки Фишборна представляют собой
геометрическую прогрессию
Для отношения 
, где 
и 
, оценки
Фишборна определяются таким образом:
Стратегия по минимизации рисков
предполагает решение задачи распределения ресурсов.
Задача решается следующим образом.
Используются две характеристики: объем финансирования ai и
полученный эффект 
Эффективность оценивается величиной 
.
При отсутствии ограничений на
финансирование строится агрегированная кривая «расходы – эффект». С этой целью
фиксируются точки кривой, соответствующие профилактическим мероприятиям с
последовательным расположением в порядке снижения эффекта. Промежуточные точки
позволяют назначать профилактические мероприятия при разных уровнях
финансирования R.
Решение сводится к определению 
, соответствующему условию
при ограничениях 
Для решения задачи используется
метод динамического программирования. Задаётся величина эффекта в зависимости
от уровня финансирования в виде кривой экспертным путем, либо экспериментально.
Зависимость соответствует степенной функции 
Агрегированная кривая «расходы – эффект» имеет вид
степенной функции 
, где B – эффект,
R – уровень
финансирования, а 
При ограниченных
ресурсах задача решается методами математического программирования
Если построение
зависимости «расходы – эффект» вызывает затруднения, то используются
эвристические правила распределения ресурсов на основе приоритетов. Известны
три группы «приоритетных» алгоритмов: 1. Абсолютных приоритетов, в которых
затраты не определяются количеством ресурсов, а назначаются опытным путем. Если
финансирование распределялось по 
, то приоритетное финансирование
определяется по зависимости 
2. Прямых приоритетов, в которых финансирование
соответствует заявленной величине 
Для снижения величины
финансирования используется зависимость
3. Обратных приоритетов, в которых финансирование
осуществляется обратно пропорционально заявленному ресурсу.
Вектор целей
организационной системы управления промышленной безопасностью (СУПБ) – это
иерархически упорядоченная совокупность целей, которые необходимо достичь.
Разность вектора целей и вектора состояния образует вектор ошибки управления.
Именно она вызывает неопределенность и, как следствие, необходимость изменений
в СУПБ, которые необходимы для повышения её эффективности.
Возможно
возникновение двух видов неопределенностей:
1) основные:
— информация о
СУПБ и окружающей ее среде;
— поведение СУПБ
во времени;
— воздействие
среды на СУПБ;
— воздействие СУПБ
на среду;
— концептуализация
информации, полученной субъектом исследования;
— восприятие
субъектом управления модели СУПБ;
2) второстепенные:
— воздействие
субъекта исследования на СУПБ и окружающую среду;
— степень влияния
модели СУПБ на субъект исследования;
— взаимодействие
субъекта исследования и субъекта управления;
— воздействие СУПБ
и среды на субъект управления.
Совершенствование СУПБ в
направлении повышения эффективности проводится по двум взаимосвязанным
направлениям: — непосредственно СУПБ управления; — стратегические направления
управления.
На рисунке представлена модель,
основные факторы которой субординированы по их принадлежности к внешним и
внутренним факторам.
Логистический анализ изменений СУПБ
требует решения вопроса их классификации
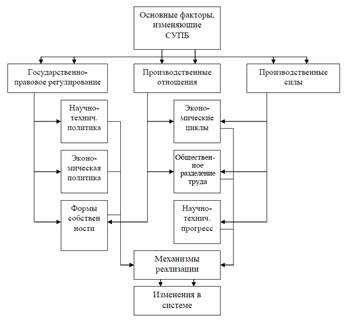
Рисунок – Модель повышения действенности
СУПБ за счёт внесения в неё изменений
С этой целью был использован XYZ-анализ. К
классу X отнесены
изменения, характеризующиеся стабильностью, с небольшими колебаниями и
возможностью их прогнозирования с высокой степенью точностью. К классу Y отнесены
изменения, характеризующиеся поддающимися учету со средними возможностями
прогноза. К классу Z отнесены
изменения, характеризующиеся отсутствием тенденций к изменениям и в следствии
этого неточным прогнозированием оценок. Способом классификации по классам XYZ является
метод, использующий коэффициент вариации 
XYZ-анализ (AZ-анализ)
позволяет осуществить 9 видов изменений. Вид определяет значимость изменений.
В таблице приведены виды изменений
по AZ-анализу,
где С – величина изменения,
– значение коэффициента вариации.
Таблица – Формирование классов изменений
СУПБ (AZ-анализ)
|
Классы измерений |
||
|
AX
|
AY
|
AZ
|
|
BX
|
BY
|
BZ
|
|
CX
|
CY
|
CZ
|
Классификация изменений позволяет
повысить действенность СУПБ наиболее эффективным образом.
ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ:
1.
Федеральный Закон «О промышленной безопасности опасных производственных
объектов» от 21.07.1997 № 116-ФЗ.
2.
Федеральные нормы и правила в области промышленной безопасности «Правила
безопасности в нефтяной и газовой промышленности», утвержденные приказом
Ростехнадзора от 12.03.2013 № 101.
3.
Федеральный закон от 22.08.1995 №151-ФЗ «Об аварийно-спасательных службах и
статусе спасателей».
4.
Федеральный Закон от 21.12.1994 г. 68-ФЗ «О защите населения и территорий от
чрезвычайных ситуаций природного и техногенного характера».
5.
Постановления Правительства РФ от 04.09.2003 № 547 «О подготовке населения в
области защиты от чрезвычайных ситуаций природного и техногенного характера».
6.
Стандарт Компании «Интегрированная система управления промышленной безопасностью,
охраной труда и окружающей среды» №П3-05 С-0009 версия 3.00.
