О СОЧЕТАНИИ СЛУЧАЙНЫХ ПРОЦЕССОВ ВЕТРОВЫХ И СНЕГОВЫХ НАГРУЗОК НА СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ

     
Задача
о сочетании случайных нагрузок на строительные конструкции рассматривалась в
многочисленных работах с представлением нагрузок в виде различных
математических моделей, описывающих вероятностную основу нагрузок. В настоящей
работе для решения названой задачи использованы методы корреляционной теории
случайных функций и теории выбросов. В частности,  приняты к рассмотрению
результаты исследования статистических характеристик нормальных случайных
процессов ветровой и
снеговой  нагрузок,
полученные на основе конкретных статистических данных многолетних
метеонаблюдений в северных регионах Западной Сибири.

     
Случайные процессы скорости ветра  и
ветрового напора обладают
свойством стационарности с постоянными во времени математическим ожиданием,
дисперсией и
нормированными корреляционными функциями соответственно:

Здесь
 характеризует
степень затухания функции , -коэффициенты,
зависящие от

     
Для случайного процесса снеговой нагрузки   свойственен
накопительный в течение зимнего периода характер и, как следствие,
нестационарность с переменными математическим ожиданием и дисперсией Процесс представляется
в виде  Здесь — полином
3-й степени, аппроксимирующий—
единичный стационарный случайный процесс.  Для принята
корреляционная функция вида . 
Параметры  определяются
в зависимости от данных метеонаблюдений за снеговой нагрузкой.

    
Суммарное одновременное воздействие на конструкцию двух нагрузок или их
сочетание характеризуется параметром ,
являющимся линейной комбинацией случайных процессов этих нагрузок. Здесь —
постоянные коэффициенты, зависящие от конструкции, воспринимающей нагрузки. 
Таким образом, решение задачи о сочетании нагрузок сводится к отысканию
вероятности того, что процесс  превысит
некоторый уровень на
отрезке времени (0-Т):  В [1] предложено
решать эту задачу аналогично задаче о вероятности выброса значений случайного
процесса за определенный уровень.

     
Используя формулу Райса  для среднего числа превышений процессом  значения
 в
единицу времени, и пренебрегая 2-кратным, 3-кратным и т.д. превышением уровня  (т.к.
для отказа конструкции достаточно 1-кратного превышения нагрузкой уровня),
запишем выражение для искомой вероятности приближенно [1]:

                
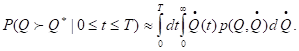
(1)

Здесь—
совместная плотность вероятности  процесса     и его
производной .

     
Случайные процессы приняты
нормальными, что позволяет  принять закон нормального распределения и для
процесса  После
ряда преобразований с учетом вышеназванных особенностей процессов нагрузок,
окончательно получим для (1):

.     
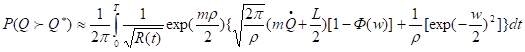(2)

Здесь
—
определитель матрицы корреляционных моментов процесса  и его
производной —
математическое ожидание процесса производной —
параметры, зависящие от вида функцийуровнякоэффициентов
—
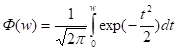табличное значение интеграла вероятности. Интегрирование (2) производится
численно. Если уровень суммарной нагрузки  является недопустимым для конструкции,
т.к. вызывает в ней предельное состояние, то характеристика ее надежности, как
вероятность не появления этого состояния

                                   (3)

    
Ниже следует пример вычисления   для ж/бетонной
колонны крайнего ряда одноэтажного промышленного здания,  воспринимающей 
одновременно распределенную по высоте ветровую нагрузку и
сосредоточенную в оголовке колонны нагрузку от снега  (при
сетке колонн здания 6х18м). С учетом параметров жесткости сечений колонны в ее
надкрановой и подкрановой частей, получим:  т.е.  По (2)
вычислялись вероятности превышения нагрузкой на
колонну уровня при
разных уровнях нагрузок Использовались
параметры процессов нагрузок и их корреляционных функций для станции Уренгой по
результатам 28 лет метеонаблюдений за климатом. Максимуму математического
ожидания процесса снеговой нагрузки соответствует t=15 декад (31 марта). Это
наиболее вероятное время одновременного действия максимумов двух нагрузок.
Расчеты ,
приведенные в нижеследующей таблице, показывают, что вероятности одновременного
превышения нагрузками  уровней
их нормативных и расчетных значений невелики, а характеристика надежности
конструкции колонны при этих уровнях сохраняет высокие значения.

     
Полученные результаты позволяют по иному подойти к вопросу учета сочетания
ветровых и снеговых нагрузок, используя не коэффициенты сочетаний, а требуемое
значение характеристики надежности конструкции.

Литература

1.    
Болотин В.В. О сочетании  случайных нагрузок,
действующих на сооружение.- Строительная механика и расчет сооружений, 1962,№2,
с.1-5. – Текст: непосредственный.

2.    
Ржаницын А.Р. Теория расчета строительных
конструкций на надежность. М., Стройиздат, 1978,239с.- Текст: непосредственный.

Literature

1. Bolotin V.V. On the combination of random loads
acting on the structure.- Construction mechanics and calculation of structures,
1962, No. 2, pp.1-5. — Text: direct.

2. Rzhanitsyn A.R. Theory of calculation of building
structures for reliability. M., Stroyizdat, 1978.239 p. — Text: direct.