Диофантовы
уравнения – это алгебраические уравнения или системы алгебраических уравнений с
целыми коэффициентами, для которых необходимо найти целые или рациональные
решения. При чем число неизвестных в уравнениях должно быть не менее двух
(если не ограничиваться только целыми числами). Диофантовы уравнения имеют
много решений, по этой причине их называют неопределенными уравнениями.
История
Диофантовы
уравнения связаны с именем древнегреческого математика Диофанта
Александрийского. О подробностях его жизни почти ничего не известно. В одном
случае, Диофант цитирует Гипсикла (2 век до нашей эры); в другом — о Диофанте
пишет Теон Александрийский (около 350 года нашей эры). Отсюда можно сделать
вывод о том, что его жизнь проходила в границах этого периода. Возможное конкретизирование
времени жизни Диофанта обосновано тем, что его «Арифметика» посвящена «достопочтеннейшему
Дионисию». Предполагают, что Дионисий — епископ Дионисий Александрийский,
который жил в середине 3 века нашей эры. В Палатинской антологии содержится
эпиграмма-задача, в которой сообщается:
Прах
Диофанта гробница покоит; дивись ей и камень
Мудрым
искусством его скажет усопшего век.
Волей
богов шестую часть жизни он прожил ребенком.
И
половину шестой встретил с пушком на щеках.
Только
минула седьмая, с подругой он обручился.
С
нею, пять лет, проведя, сына дождался мудрец;
Только
полжизни отцовской возлюбленный сын его прожил.
Отнят
он был у отца ранней могилой своей.
Дважды
два года родитель оплакивал тяжкое горе,
Тут
и увидел предел жизни печальной своей.
Решение
данной задачи наводит на мысль о том, что Диофант прожил 84 года. До нас дошли
7 книг Диофанта из (возможно) 13, которые были объединены в сборник задач (их
всего 189) под названием «Арифметика», каждая из которых обеспечивает решением
и необходимым пояснением.
Метод
решения уравнения с двумя переменными как квадратного относительно одной из
переменных
Пример
№1
Решить
уравнение в целых числах:
Решение.
Рассмотрим уравнение как квадратное относительно 
Чтобы
уравнение имело решения, требуется, чтобы 
.
Вероятно
это при 
в
таком случае 
Ответ:
Пример
№2
Решить
уравнение в целых числах:
Решение.
Стремиться выделить полные квадраты в левой части исходного уравнения очень
сложная и долгая задача.
Найти
разложение левой части на множители методом группировки также нелегко. Поэтому пробуем
разложить на множители, рассматривая исходное уравнение как квадратное
уравнение относительно одной из переменных, в то же время, надеясь, что его
дискриминант будет полным квадратом. Перепишем исходное уравнение в виде:
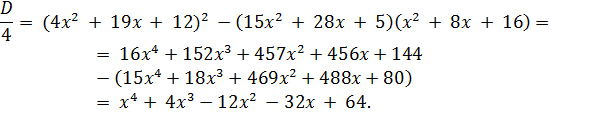
Далее
упростим 
,
найдя корни многочлена 
.
Затем решаем уравнение 
Разделив
обе части на
,
имеем:
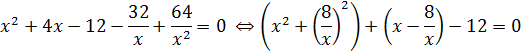
Пусть
в
таком случае
Откуда
А
отсюда:
примет
вид
Получается,
Заметим,
что это же выражение для дискриминанта можно было бы получить гораздо проще,
если бы перед всеми вычислениями квадратные трехчлены 
разложили
на множители. Таким образом, решениями квадратного (так как коэффициент при
старшей степени 1
)
уравнения являются
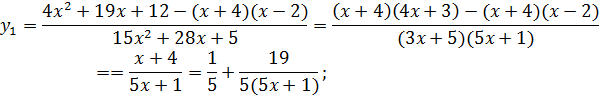
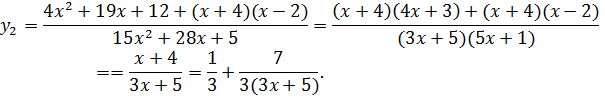
Потому
как 
,
то, по крайней мере, 
должно
быть делителем числа 
.
Следовательно,
имеют место лишь четыре возможности:
±1,
целыми
числами является 
тогда
тогда
4.
Итак,
определили две пары 
которые
являются решением.
Точно
так же приходим к выводу, что 
тогда
целочисленным решением будет 
и,
следовательно, 
.
Ответ
Метод
бесконечного (непрерывного) спуска
Методом
бесконечного спуска называют рассуждения, которые проходят по следующей схеме:
предполагаем, что у задачи есть решения, затем строим определенный бесконечный
процесс, тогда как по самому смыслу задачи он обязан на чём-то закончиться. Зачастую
данный метод применяется в более простой форме. Положив, что мы уже добрались до
естественного конца, замечаем, что «остановиться» не можем.
Пример
№1
Докажем
неразрешимость в натуральных числах уравнения:
Решение.
Предположим, что решение есть, и 
решение
с наименьшим возможным 
Из
вида уравнения следует, что 
.
Подставим решение в уравнение, затем сократим на 2:
Получили,
что 
,
следовательно,
Точно
так же, 
,
и,
Следственно,
–
также решения нашего уравнения. Но 
,
а это противоречит выбору исходного решения. Отсюда следует, решений нет.
Ответ:
Решений нет.
Из
приведенного выше доказательства видно, что применение метода спуска в данном
примере опирается на тот факт, что любое непустое множество натуральных чисел
имеет минимальный элемент. Иначе говоря, данный метод заключается в построении
бесконечной последовательности убывающих целых положительных чисел. Так как убывающая
последовательность целых положительных чисел имеет лишь конечное число членов,
мы получаем противоречие.
Пример
№2
Найти
все решения в натуральных числах уравнения:
Решение.
Обратим внимание на то, что 
–решение
исходного уравнения. Из тождества 
получаем,
что пара 
–
решение, а значит и пара 
–
тоже решение. Определена бесконечная последовательность решений 
и
т.д.
Докажем,
что других пар чисел, которые удовлетворяют исходному уравнению, нет. Пусть –
некоторое решение. Из тождества 
следует,
что 
–
также решение.
Из
условия задачи 
имеем,
что 
.
При 
,
из условия задачи 
следует,
что 
То
есть при ,
мы из решения 
,
получаем
решение 
в
натуральных числах, при этом 
.
Когда-нибудь будет получено решение 
так
как этот процесс не может продолжаться бесконечно.
Из
условия задачи следует, что 
.
Значит 
Вследствие
этого, 
,
а значит, числа 
принадлежат
построенной ранее последовательности.
Ответ.
–
решение уравнения.
ЗАКЛЮЧЕНИЕ:
Данная
работа несет методический характер и может быть полезной в различных кружковых
работах (по математике).
СПИСОК
ЛИТЕРАТУРЫ:
1.
Abakumova, S. I. Diofantovy uravnenija /
S. I. Abakumova, A. N. Guseva // Fundamental’nye i prikladnye issledovanija v
sovremennom mire. – 2014 – T. 1, №6. – S. 133–137.
2.
Bazylev D.F. Spravochnoe posobie k
resheniju zadach: diofantovy
3.
Bashmakova I.G. Diofant i diofantovy
uravnenija. – M.: «Nauka», 1972 g.
4.
Grin’ko E.P., Golovach A.G.
Uchebno-metodicheskoe posobie. Metody reshenija diofantovyh uravnenij pri
podgotovke shkol’nikov k olimpiade. Brest BrGU imeni A.S. Pushkina, 2013
5.
uravnenija. – Minsk: NTC «API», 1999 g.
6.
Falin G.I., Falin A.I. Linejnye diofantovy
uravnenija. M., Izd-vo Chistye Prudy, 2008, 32 s. (bibliotechka «Pervogo
Sentjabrja», serija matematika, vyp.24).
