Н е р а в е н с т в о Г ё л ь д е р а .
Теорема. Пусть ![]()
![]() ;
; ![]() ,
,
причем ![]() .
.
Тогда

Замечание. Числа ![]() и
и ![]() называются сопряженными показателями, если
называются сопряженными показателями, если ![]() .
.
Д о к а з а т е л ь с т в о .
Для доказательства неравенства Гёльдера, нам понадобится следующее утверждение:

Оно справедливо в силу неравенства между взвешенными средним арифметическим и средним геометрическим для двух чисел:
![]()
Положим
![]()
Имеем
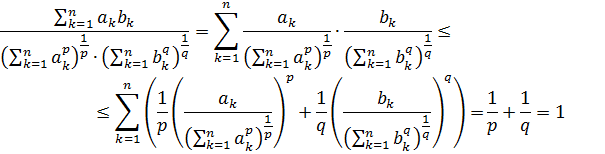
Мы получили, что
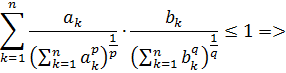
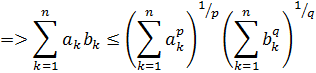
Что и требовалось доказать.
С л е д с т в и е .
В случае, когда ![]() получается неравенство Коши – Буняковского – Шварца для сумм
получается неравенство Коши – Буняковского – Шварца для сумм ![]() :
:
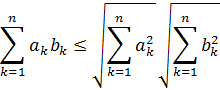
П р и м е р 1 .
Пусть ![]() и
и ![]() – положительные числа такие, что
– положительные числа такие, что ![]() . Доказать, что
. Доказать, что ![]()
Р е ш е н и е .
Положим
![]()
Тогда правая часть нашего неравенства ![]() будет равна
будет равна
![]()
Возьмем теперь
![]()
Так как
![]()
то
![]()
Аналогично
![]()
![]()
Теперь, пользуясь неравенством ![]() , получим:
, получим:
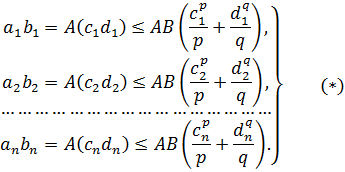
Из этих неравенств следует, что

Итак, доказано, что левая часть неравенства ![]() не превосходит правой части, т.е.
не превосходит правой части, т.е. ![]() .
.
Список использованной литературы.
1. Беккенбах Э., Беллман Р. Введение в неравенства. 1965.
2. Вавилов В. В. Задачи по математике. Уравнения и неравенства. 2007.
3. Калинин, С. И. Средние величины степенного типа. Неравенства Коши и Ки Фана: Учебное пособие по спецкурсу. 2002.
4. Коровкин П. П., Неравенства.1996.
5. Некоторые вопросы математического анализа и методики его преподавания: Сб. научн. статей. Киров: Издательство ВГГУ, 2001.
6. Харди, Г.Г. Неравенства. 1948.

