На сегодняшний день, несмотря на развитие современных технологий, остаются нерешенными некоторые проблемы, с которыми человечество сталкивается каждый день. К одной из таких проблем можно отнести управление системой автомобильного транспорта и дорожными сетями поселений. Транспорт, как один из важнейших аспектов жизни современного города, имеет непосредственное отношение к каждому жителю. Достаточно перечислить его функции, начиная с обеспечения связи с жизненно важными пунктами (больницы, полицейские и пожарные участки), доставки продовольствия и необходимых товаров, и заканчивая рядовой поездкой на работу, учебу, место отдыха и т.д. Жизнь города сейчас не представляется возможной без хорошо организованной дорожной системы.
Для осознания сложности задачи оптимизации транспортных потоков стоит указать ряд вопросов, периодически возникающих в дорожной сети: прокладка новых дорог и соответствующие изменения в распределении транспортной нагрузки смежных секторов [1], своевременный ремонт и расширение дорожного покрытия, сопряженное с временными затруднениями при проезде [2], установление графика движения общественного транспорта для участков проектирования новых деловых, общественных или жилых центров [3], оптимизация движения на существующих участках [4]. Список этих практических задач ещё можно продолжить. Для дорожной сети мегаполиса это становится серьезной задачей, для решения которой требуются специальные системы управления, основанные на моделях и алгоритмах математического моделирования транспортных потоков. При этом сами модели должны быть в достаточной степени точны и учитывать большое количество факторов: погодные условия, время суток, плотность потока, состояние дорожного покрытия и самого ТС, что делает вычисления достаточно сложными. Таким образом, в данной статье будет предложено математическое и программное решение задач моделирования транспортных потоков городов с точки зрения актуальности рассмотрения практических аспектов, концепции рационализации транспортных сетей в крупных городах России.
Руководствуясь личным опытом вождения автомобиля, хочется отметить, что большая загруженность транспортной сети является результатом позднего перестроения водителей (это регулируется нанесением сплошных линий разметки, обозначающих полосы движения в пределах перекрёстка), а также неизменной длительностью работы фаз светофора и неспособностью водителей подстраиваться под них. Участники движения, совершающие поздний маневр, заставляют остальных участников движения сбавлять скорость, что приводит к «подвижной пробке». Светофоры, работающие с постоянной длительностью фаз вне зависимости от времени суток или дня недели, являются причиной образования пробок, поскольку потоки автотранспорта в разное время могут иметь абсолютно разную интенсивность и даже направление.
Для решения проблемы совершенствования дорожного движения города разработан методический подход, благодаря которому возможна реализация оптимизационного эксперимента на основе модели светофора с изменением длительности фаз работы.
Обозначим классический четырёхзначный перекресток как Crossroad, выделим четыре главных направления, как показано на рисунке 1. По назначению разобьем районы следующим образом:
· A– деловые районы (офисы, фирмы, магазины);
· B– государственные учреждения (школы, поликлиники);
· C– места отдыха (парки, дачные поселки, точки питания);
· D– спальные районы (место проживания ≈ 70% жителей).
Рассмотрим разные дни недели и время суток, а также соответствующие им приоритетные направления:
· будние дни – утро –A и B; будние дни – вечер – C и D;
· выходные дни – утро – С и D; выходные дни – вечер – D.
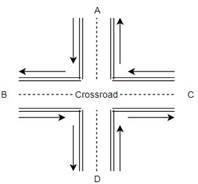
Рис. 1. Перекресток Crossroad с различными приоритетными направлениями
Отметим, что преимущественные направления движения меняются достаточно часто, и этот фактор следует учитывать при работе светофоров в данных направлениях.
Возьмем светофор с тремя цветовыми сигналами: зеленым, желтым и красным, обозначим черезtg, ty и tr длительность наблюдения каждого цвета соответственно. Согласно ГОСТ [5] время работы некоторых фаз светофора фиксировано: длительность фазы желтого сигнала должна быть равна трем секундам. Имеем некоторые ограничения, накладываемые на время работы фаз светофора:
1. ty = 3с.
2. try < 2c.
3. tg > min{ tA, tB, tC, tD, tE }, где в правой части значения длительности временных интервалов, достаточных для проезда через светофор хотя бы одного транспортного средства определенной категории, которым разрешено движение.
Данные ограничения позволяют избежать ситуаций, когда времени работы сигнала светофора недостаточно для преодоления перекрестка.
Необходимо найти числовое значение, отображающее отношение длительности разрешающего и запрещающего сигналов. Поскольку длительность «желтого» нельзя изменять, то будем исследовать только отношение зеленого и красного сигналов, которое обозначим как k. Пусть плотность транспортного потока, приближающегося к светофору, равна p, тогда, согласно макроскопическим моделям можно рассчитать скорость распространения информации о торможении транспортных средств:
|
|
(1) |
где 
– максимально возможная плотность транспортных средств на данном участке дороги и 
– значение потока АТС.
Далее представляется возможным вычислить количество АТС, которое будет накапливаться за время горения запрещающего сигнала светофора:
|
|
(2) |
Длительность включения зеленого сигнала светофора, обеспечивающую пропускную способность через перекресток всех скопившихся автомобилей и предотвращающую увеличение их количества, можно представить в виде неравенства:
Следовательно, регулируя значение k, можно устанавливать различные длительности фаз работы светофора, тем самым ускоряя прохождение транспортных потоков в разное время суток в зависимости от приоритетности направления. Эта схема частично решает вопрос об изменении длительности фаз работы светофора, но не учитывает перестроения при подъезде к светофору, что в итоге значительно влияет на фактор плотности. Поэтому для высокого качества оптимизации конкретного перекрестка следует, сначала вычислить изменение плотностей АТС, возникающих при перестроении, и только потом применять данное отношение.
Регулирование фаз работы смежных светофоров при внесении изменений
При поправке времени работы одного конкретного светофора, необходимо помнить о наличии и последующих светофоров в направлении движения транспортного потока. Вдобавок необходимо помнить, что светофор, работающий по принципу изменения длительности фаз работы пропускает больший поток АТС в приоритетном направлении движения. Следовательно, для обеспечения быстрого прохождения заданного участка дороги необходима корректировка фаз работы смежных.
Рассмотрим участок автодороги, на котором расположено n светофоров, идущих один за другим на заданном расстоянии друг от друга. Присвоим им нумерацию в порядке их проезда, начиная от 1 и заканчивая n. Для каждого светофора определим время работы его сигналов tr, tg и ty, задающее красный, зеленый и желтый цвет соответственно. Определим общее время для полного цикла работы светофора ttot = tr + tg + 2ty. Сначала рассмотрим ситуацию с синхронизацией двух соседних светофоров i и i + 1, где i ∈ 1 : n − 1, далее полученные выводы обобщим на весь участок рассматриваемой дороги.
Принимая во внимание ситуацию функционирования соседних светофоров, дополнительно введем t∆i,i+1, равное разности начал циклов работы ttot светофоров i и i + 1. Также определим отношение времени работы зеленого и красного сигналов светофоров ki. Таким образом, задача сводится к минимизации простоя АТС перед следующим светофором при изменении параметров ki и ttot на рассматриваемом участке дороги. Обозначим общее суммарное время ожидания всех автотранспортных средств на перекрестке как tstop.
Учитывая значения рассмотренных выше параметров и описав движение потока, можно создать математическую модель для расчета оптимального времени проезда автотранспортных средств. Для описания движения будет целесообразно задать следующие параметры:
· Si,i+1– расстояние между светофорами i и i + 1;
· L – средняя длина кузова АТС в потоке;
· dmin– минимальное безопасное расстояние между двумя соседними АТС в потоке,
· dmin> L + dτ+ dl, где dτ– расстояние, которое пройдет автомобиль за время реакции водителя τ, а dτ– за время торможения в модели следования за лидером;
· Vi,i+1– скорость движения АТС на рассматриваемом участке, которую будем считать постоянной;
· ti,i+1– время проезда участка дороги длиной Si,i+1, ti,i+1= Si,i+1/Vi,i+1;
· tsafe – интервал безопасного движения между соседними автомобилями, которое можно задать формулой tsafe = dmin/Vi,i+1;
· ag – количество автомобилей, проехавших светофор за время tg.
Рассмотрим различные варианты движения АТС, которые могут возникнуть при проезде светофоров на заданном участке.
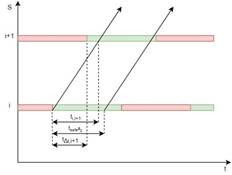
Пример 1. Пусть t∆i,i+1∈ [,ti,i+1; ti,i+1+ tr].
В данном случае все машины, проехавшие светофор i, подъезжающие к красному сигналу светофора i + 1, вынуждены ожидать зеленого сигнала и проезда автомобилей, стоящих перед ними, как показано на рисунке 2.
Рис. 2. Проезд светофора с прибытием на красный сигнал и простоем
Исходя из данных изображения, становится очевидной формула для вычисления времени простоя автотранспортных средств на светофоре tstop:
|
tstop= ag (t∆i,i+1− ti,i+1) |
(4) |
Пример 2. Пусть t∆i,i+1∈ [,ti,i+1+ tr; ti,i+1+ tr + agtsafe]. Данная ситуация соответствует случаю, когда только часть автомобилей, находящихся перед светофором, успела проехать перекресток на зеленый сигнал.
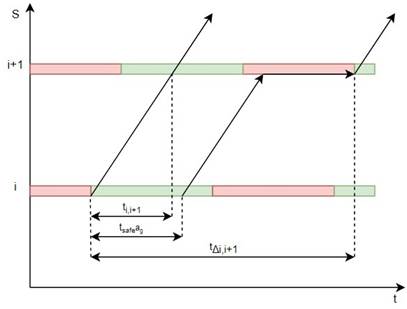
Рис. 3. Проезд светофора с частичным простоем
На основе данных рисунка 3 можно вывести формулу для вычисления общего времени простоя:
где ar – количество автомобилей, остановившихся на светофоре i+1, которое можно выразить следующим образом:
|
|
(6) |
Пример 3. Пусть t∆i,i+1∈ [,ti,i+1+ tr + agtsafe; ti,i+1 + ttot]. В этом варианте разница во времени в циклах работы светофоров попадает в промежуток, достаточный для достижения транспортным потоком следующего светофора, при том, что следующий цикл работы зеленого сигнала светофора i + 1 будет включать время, необходимое для проезда всех автотранспортных средств. Таким образом, последний рассматриваемый временной интервал будет соответствовать событию прямого проезда участка дороги без задержек и простоев на следующем светофоре. Данный случай наглядно демонстрируется на рисунке 4.
Рис. 4. Проезд светофора без простоя
Очевидно, что в рассматриваемом временном интервале простоя на следующем светофоре нет, поэтому время ожидания движения tstop = 0.
Полученные результаты и зависимость tstop от t∆i,i+1 по формулам 4 и 5 можно изобразить графически, как показано на рисунке 5, при этом максимальное время простоя tstop будет равно ag (t∆i,i+1 — ti,i+1):
Рис.5. График зависимости tstop от t∆i,i+1
Несомненно, наилучшим вариантом из рассмотренных будет случай tstop = 0. Тогда становится возможным составление алгоритма действий по расчету диапазона значений оптимальной разности во времени работы соседних светофоров для минимизации простоя и заторов перед светофором.
Методика включает следующие этапы:
1. Определение значения необходимых параметров ttot, Si,i+1, L, dmin, Vi,i+1, ti,i+1, tsafe, ag.
2. Расчет значения оптимального параметра k при фиксированном ttot по формуле 3, рассмотренной ранее.
3. Определение значения tg, tr.
4. Вычисление границы значений t∆i,i+1, внутри которых tstop будет минимальным.
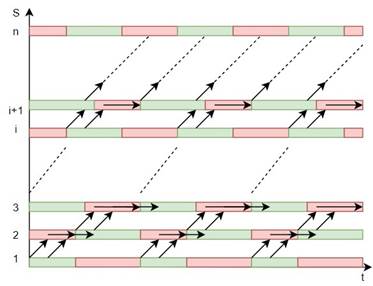
Данный метод применим при исследовании модели двух соседних светофоров, поэтому полученные выводы стоит обобщить на случай установления работы светофоров на целой улице, участке района или автомагистрали. Приведем пример такого участка, включающего n светофоров, на рисунке 6:
Рис. 6. График движения и простоя транспорта на участке дороги
Необходимо оптимизировать проезд по данному отрезку дороги с целью уменьшения времени простоя автотранспортных средств. По очевидным причинам, нельзя задать одновременное смещение фаз работы всех светофоров на заданном участке, поскольку это действие приведет к резкому ухудшению дорожной ситуации для автомобилей, следующих по маршруту на тот момент.
Следовательно, нужно перестраивать работу светофоров постепенно, в несколько этапов. Во-первых, быстрый проезд рассматриваемого отрезка пути будет достигаться установкой одинакового цикла работы всех светофоров, чтобы смещение в разнице циклов не приводило к дальнейшим заторам. Во-вторых, оптимальная разница в фазах работы должна устанавливаться на протяжении некоторого количества времени во избежание долгого простоя следующих по дороге автомобилей.
Для решения этих проблем потребуется ввести несколько дополнительных переменных: 
– длина цикла работы светофора i, 
– максимально возможное время смещения фаз работы светофора i, не приводящее к затору. Теперь можно приступать к созданию алгоритма перенастройки режима работы для большого участка дороги, который будет состоять из следующих этапов:
1. Определить «проблемный» участок дороги {m − 1, m, m + 1}, m ∈ 2 : n − 1, на котором образуется неподвижная пробка или затор, с изучением значения плотностей транспортного потока вблизи светофоров.
2. Рассчитать возможные границы значения 
∈
, где – оптимальная длина цикла работы светофора, с возможностью задать значение k по формуле 3, при котором не образуется пробка.
3. Измерить длину циклов ∈ N, i ∈ 1 : n. Рассчитать среднее значение, округленного до целого числа секунд, 
3.1. Если 
3.1.1. Если 
, то значение уменьшить на 
.
Вернуться в начало шага 3.
3.1.2. Если 
, то значение увеличить на .
Вернуться в начало шага 3.
3.1.3. Если 
, то перейти к шагу 4.
3.2. Если 
, увеличить i ∈ 1 : n на .
Вернуться в начало шага 3.
3.3. Если 
, увеличить i ∈ 1 : n на .
Вернуться в начало шага 3.
4. Вычислить
— значение 
, при котором 
минимально, используя алгоритм для соседних светофоров, рассмотренный выше.
5. Привести текущие значения , i ∈ 1 : n – 1 к оптимальным значениям по следующему принципу, разбив действия на два цикла:
5.1. В цикле по x ∈ m −1 : 1 значения 
поочередно приблизить к 
, соответственно уменьшив или увеличив его на 
.
5.2. В цикле по y ∈ m : n − 1 значения 
поочередно приблизить к 
, соответственно уменьшив или увеличив его на 
.
6. Повторять данный пункт алгоритма до тех пор, пока не будет выполнено равенство =, i ∈ 1 : n − 1.
Работа предложенного алгоритма включает данную последовательность действий: выявление проблемного участка, приведение циклов работы светофоров к одинаковому значению, приведение дальнейшего изменения в их началах к необходимому оптимальному смещению, координируя его независимым образом в противоположные стороны движения от источника затора.
К сожалению, у рассмотренной модели настройки светофоров есть свои недостатки. Она подходит только для исследования случая движения по главной дороге, при котором автомобили могут проходить на максимально разрешенной скорости без каких-либо задержек. Пример такого участка пути можно привести графически, как показано на рисунке 7:
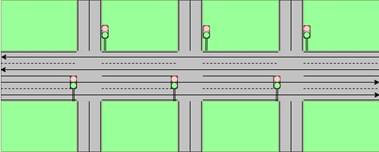
Рис. 7. Движение по главной дороге
СПИСОК ЛИТЕРАТУРЫ
1. Patriksson M. The traffic assignment problem, models and methods // VSP. –– 1994. –– P. 25–44.
2. Perlman C. Mathematical Modelling of Traffic Flow at Bottlenecks : Ph. D. thesis / Cathleen Perlman. –– 2008. –– P. 59.
3. O’Flaherty C. Transport planning and traffic engineering // Elsevier. –– 2006. –– P. 57– 62.
4. Gomes G. Optimization problems in traffic control // Mathematical modeling of traffic flows. –– Independent University of Moscow, 2015. –– P. 55.
5. «ГОСТ Р 52289-2004. Национальный стандарт Российской Федерации. Технические средства организации дорожного движения. Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств» (утв. Приказом Ростехрегулирования от 15.12.2004 N 120-ст) (ред. от 09.12.2013)), пункт 7.4.2.
