Одной из самых важных проблем, точное и окончательное решение которой до сих пор не было найдено, является проблема возникновения колебаний виляния вагонов при движении по прямому или кривому участку пути большого радиуса. Такое неустойчивое движения часто приводило к авариям и крушениям. Кроме того, поскольку такой вид движения является результатом конструктивного исполнения экипажей, оно всегда присутствует при движении поездов. Неизбежность возникновения эффекта виляния и его высокая опасность для безопасности движения делает проблему особенно актуальной.
Интенсивность виляния вагонов и локомотива зависит от той скорости, с которой движется поезд. Критическая скорость определяется так называемыми коэффициентами крипа. По своему физическому смыслу коэффициенты крипа равны производным функций сил трения в местах контакта колёс и рельсов от относительных скоростей скольжения [1, c 87]. Особое значение имеют величины этих коэффициентов, вычисленные при равенстве нулю продольных и поперечных скоростях:
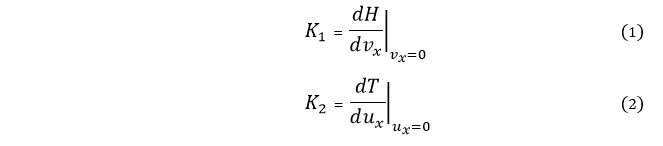

Т – продольная сила;
Н – поперечная сила;
Проблеме численного определения величин коэффициентов К1 и К2 посвящено множество работ. Широкое распространение получила следующая методика, разработанная ВНИИЖТ:
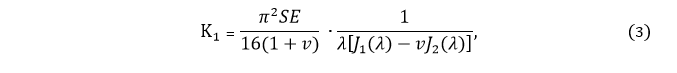
где S – площадь пятна контакта, зависящая от геометрии поверхностей катания колеса и вертикальной нагрузки, направленной от колеса на рельс (м2)
v – коэффициент Пуассона;
Е – модуль упругости стали (Па);

Зная геометрические и физические параметры элементов конструкции подвижного состава, можно оценить величины исследуемых коэффициентов по вышеизложенной методике.
Если:
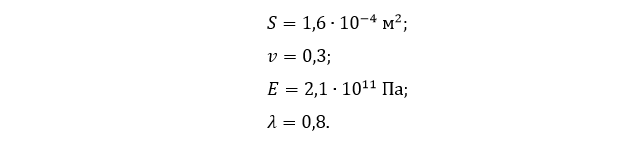
То выполняя вычисления, согласно изложенной методике, можно получить следующие результаты:
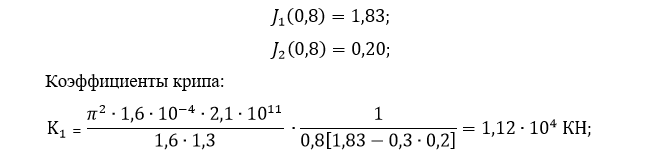

Помимо вышеизложенной методики, широко известен другой метод оценки, предложенный Ф. Картером [2, 36]. При использовании этой методики представляется возможным определить максимальное значение коэффициента крипа, используя которое в дальнейшем можно получить и минимальное, воспользовавшись эмпирической формулой.

Как можно заметить, полученные значения отношений коэффициентов крипа весьма значительно различаются. Опыт испытаний свидетельствует о том, что первый метод оценки лучше согласуется с результатами экспериментов. При его использовании теоретические значения располагаются ближе к экспериментальным.
Однако точная математическая модель отыскания коэффициентов крипа ещё не была получена. Её разработка является актуальной задачей, решение которой в значительной мере повлияет на безопасность движения поездов и позволит по-новому взглянуть на привычные конструктивные элементы подвижного состава, на этот раз, принимая во внимание параметры динамических процессов, происходящих при высоких скоростях его движения.
Библиографический список
- Котуранов В.Н., Козлов М. П. Технологическая последовательность экспертных оценок рабочих качеств универсального грузового вагона (на примере цистерны модели 15-1443): Учебное пособие. / В.Н. Котуранов., М. П. Козлов; – М.: МИИТ, 2013. – 147 с.
- Беспалько, С. В. К вопросу о моделировании продольных колебаний цистерны, частично заполненной жидкостью. / С. В. Беспалько // Вестник ВНИИЖТ. – 1999. – №4. – с. 35 – 40.

