ИНФОРМАЦИОННЫЕ ПОКАЗАТЕЛИ ЭФФЕКТИВНОСТИ АЛГОРИТМОВ РЕШЕНИЯ СИТУАЦИОННЫХ ЗАДАЧ ПЛАНИРОВАНИЯ КАРЬЕРЫ СУБЪЕКТА

21 мая 8:00

Авторы

Синицын Сергей Александрович (Российский университет транспорта )

Аннотация

Целью решения ситуационной задачи планирования карьеры субъекта является получение на основе некоторой достоверной математической модели совокупности характеристик, удовлетворяющих самой ранней стадии постановки задачи на уровне желаний субъекта, его устремлений, способностей, среды существования, материальных возможностей и прочих объективных факторов его жизни. Такая задача может быть решена только в многоуровневой или иерархической постановке, когда жизнь субъекта разбита на несколько глобальных этапов. Завершение каждого жизненного этапа субъекта формирует новый набор исходных данных для прогнозирования оптимального решения на следующем этапе. Такая гипотеза позволяет практически разбить решение глобальной ситуационной задачи на ряд самостоятельных подзадач, в каждой из которых следует оценивать область достоверных решений с помощью доверительных диапазонов.Основная группа доверительных диапазонов промежуточных состояний ситуационной задачи вычисляется в процессе решения этапа и может быть использована повторно другими субъектами, которые решают аналогичные ситуационные задачи с теми же исходными характеристиками при воздействии случайных факторов. На вход модели первого уровня, как и моделей последующих уровней, воздействуют точечные параметры характеристик и случайных факторов, а также параметры принятия решений нулевого или предыдущих уровней, которые для выполнения вычислений выбираются из соответствующих доверительных диапазонов.

Ключевые слова

ситуационные задачи, достоверные модели, многоуровневые модели, этапы решения ситуационных задач, коррекция исходных данных, прогнозирование правильных решений, доверительные диапазоны.

Annotation

The goal of solving the situational task of planning a person’s career is to obtain, on the basis of some reliable mathematical model, a set of characteristics that satisfy the earliest stage of setting the task at the level of the subject’s desires, his aspirations, abilities, living environment, material capabilities and other objective factors of his life. Such a problem can be solved only in a multilevel or hierarchical setting, when the life of the subject is divided into several global stages. The completion of each life stage of the subject forms a new set of initial data to predict the optimal solution in the next stage. This hypothesis makes it possible to practically divide the solution of the global situational problem into a number of independent subtasks, in each of which the region of reliable solutions should be estimated using confidence ranges. The main group of confidence ranges of intermediate states of the situational problem is calculated in the process of solving the stage and can be reused by other entities that solve similar situational problems with the same initial characteristics under the influence of random factors. The input parameters of the first-level model, as well as the models of subsequent levels, are affected by the point parameters of characteristics and random factors, as well as decision-making parameters of zero or previous levels, which are selected from the corresponding confidence ranges to perform calculations.

Keywords

situational tasks, reliable models, multi-level models, stages of solving situational problems, correction of initial data, forecasting of correct decisions, confidence ranges.

Дата публикации

19.12.2019

Финансирование

Располагая
соответствующими условными и безусловными плотностями распределения:

f(Pr_i^(j)/Pr_i^(j-1))
, f(Pr_i^(j)) , f(Pr_i^(j-1)/Pr_i^(j))
, …

можно
выполнить коррекцию некоторого доверительного диапазона ∆Pr_i⁽^j⁾,
вычисленного по полным вариациям характеристик модели j-го уровня:

∆Pr_i⁽^j^)*
= ∆K Mod⁽^j⁾(Pr⁽^j^-1)
, Z , ζ
), (1)

где
∆K – коэффициент разброса
характеристик модели данного уровня;

Z
– управляющие характеристики; ζ
– случайные факторы.

Для
решения задачи коррекции границ доверительного диапазона[1,c.17]
вычисляется безусловная энтропия по всему доверительному диапазону (Pr_i_,л⁽^j⁾
,Pr_i_пр⁽^j⁾)
по формуле:

H(∆Pr_i⁽^j⁾)
= — (Pr_i_,_L⁽^j⁾)
lnq(Pr_i_,_L⁽^j⁾)
, (2)

где
N – число интервалов квантования
доверительного диапазона i-го
параметра на j-м этапе моделирования.

Далее
вычисляется поправка границ доверительного диапазона за счет статистических
связей, если таковые имеются, — поправка условной энтропии:

∆H(Pr_i⁽^j⁾/Pr_i⁽^j^-1))
= — (Pr_i⁽^j^-1)/Pr_i_,_L⁽^j⁾)dPr_i⁽^j^-1)x(Pr_i⁽^j⁾)dPr_i⁽^j⁾x

xlog[(Pr_i⁽^j^-1)/Pr_i_,_L⁽^j⁾)dPr_i⁽^j^-1)/(Pr_i⁽^j^-1)/Pr_i_,_L⁽^j⁾)dPr_i⁽^j^-1)
. (3)

В
выражении (3) интегралы могут быть заменены числовыми значениями вероятностейq(Pr_i⁽^j^-1)/Pr_i_,_L⁽^j⁾)
если распределение задано численно, а не функционально [2,c.212].

Таким
образом, условная энтропия параметра принятия решения Pr_i⁽^j⁾определяется
по формуле:

H(Pr_i⁽^j⁾/Pr_i⁽^j^-1))
= H(∆Pr_i⁽^j⁾)
— ∆H(Pr_i⁽^j⁾/Pr_i⁽^j^-1)).
       (4)

Согласно
соотношению (4) условная энтропия меньше безусловной H(∆Pr_i⁽^j⁾),
а приведенный доверительный диапазон j-го
состояния соответствует величине:

∆Pr_i^(j) = 0,5exp H(Pr_i^(j)/Pr_i^(j-1)).
                        (5)

Границы
приведенного диапазона фиксируются путем привязки к математическому ожиданию
параметра принятия решения Pr_i⁽^j⁾.

После
вычисления границ доверительного диапазона следует провести дополнительный
анализ полученных результатов на предмет выполнения необходимых условий их
достоверности [3,c.86].

Во-первых,
величина полученного диапазона должна быть меньше, чем на предшествующем этапе
моделирования.

Во-вторых,
правая и левая границы нового доверительного диапазона ∆Pr_i⁽^j⁾
не должны выходить за пределы границ диапазона предыдущего уровня ∆Pr_i⁽^j^-1),
как показано на рис.1.

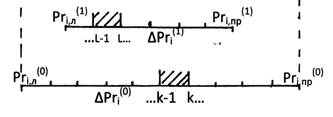
Рис.1.
Геометрическая интерпретация достоверного решения

В
случае выхода одной из границ доверительного диапазона параметра текущего
уровня моделирования ∆Pr_i⁽^j⁾за
пределы границ диапазона предыдущего уровня ∆Pr_i⁽^j^-1)
решение задачи следует повторить на том же этапе, расширив границы
доверительного диапазона предыдущего уровня ∆Pr_i⁽^j^-1),
чтобы избежать возможной потери правильных решений. Здесь необходимо помнить,
что точность приведения доверительного диапазона по вычисленной условной
энтропии произвольного распределения вероятностей соответствует энтропии
равномерного распределения [4,c.32].

На
промежуточных этапах решения не представляется важным точное соответствие
энтропии каждого параметра заданным значениям, поэтому здесь целесообразно
использовать осредненные оценки информации. Иными словами, в результате
вычисления диапазонов ∆Pr_i⁽^j⁾
на каждом этапе можно вычислить суммарную остаточную неопределенность
ситуационной задачи:

H(Pr⁽^j⁾/Pr⁽^j^-1))
= (∆Pr_i⁽^j⁾/Pr⁽^j^-1)),
                           (6)

где
n – количество параметров j
– го этапа решения.

Приобретенное
количество информации определяется разностью условных энтропий соседних этапов
решения задачи:

∆Inf(Pr⁽^j⁾/Pr⁽^j^-1))
= H(Pr⁽^j^-1)/Pr⁽^j^-2))
– H(Pr⁽^j⁾/Pr⁽^j^-1))
. (7)

На
основании формулы (7) вычисляется градиент количества информации, который
определяет эффективность решения любой ситуационной задачи, поставленной перед
субъектом [5,c.177].

Трудность
выстраивания алгоритма решения ситуационной задачи состоит в том, что процесс
решения строится по многоэтапной, иерархической схеме. В связи с чем, и сами
модели должны быть многоэтапными и соответствовать процессу решения [6,c.77].
Здесь возникла задача привязки математических моделей к процессу решения на
основе количественных факторов, которые разработаны с привлечением меры
количества информации.

В
наших задачах широко применяются многоразмерные стохастические и реже
детерминированные модели с модульной структурой [7,c.199],
которые позволяют выполнять, в случае необходимости, замену отдельных блоков.
Многоразмерность моделей порождает значительные трудности в оценке их свойств,
в плане соответствия этапу моделирования. Кроме того, принятая в нашем
исследовании схема оценки доверительных диапазонов подразумевает, как наличие
самого диапазона, так и законов распределения вероятностей на этом диапазоне.
Чтобы избежать трудностей решения задач векторной оптимизации, для оценки
эффективности такого класса моделей, здесь предложен информационный подход.
Обобщенная задача исследования моделей оценок распадается на две задачи.

Первая
задача связана с разработкой сравнительных критериев эффективности, полученных в
виде показателей прироста количества информации ∆Inf(Pr).

Вторая
задача связана с определением показателей достоверности оценочных моделей для
различных этапов решения [8,c.70].

Здесь
обе оценки сливаются в единую оценку достоверности результатов решения
ситуационной задачи. Соответствие критериев получено на основании общих
характеристик параметровPr_i⁽^j⁾
и их доверительных диапазонов ∆Pr_i⁽^j⁾.
Каждое состояние решения ситуационной задачи характеризуется доверительными
диапазонами, а не самими реализациями параметров, различные значения которых
вполне вероятны в границах вычисленных доверительных диапазонов. Совокупной
оценкой всех диапазонов одного уровня решения является информация. Аналогичный
критерий существует и для модели оценки, число параметров которой может быть
меньше количества характеристик данного этапа решения задачи.

Список
литературы

1.Синицын
С.А. Информационный критерий достоверности этапа решения ситуационной
задачи//Евразийский союз ученых (ЕСУ): ежемесячный научный журнал №10 (67), 3
часть, 2019. — с. 15-18.

2.Синицын
С.А. Задача синтеза геометрической информации при оптимальном моделировании
гладких дифференциальных поверхностей//
Инновации и инвестиции. 2018. № 10. С. 211-214.

3.Левчук
Т.В., Казаков М.С., Зверев А.С. Оптимизация систем массового обслуживания//
История и перспективы развития транспорта на севере России. 2014. №1. С.84-87.

4.Левчук
Т.В., Маслов А.А. Использование имитационного моделирования для анализа
эксплуатационных испытаний программного обеспечения// История и перспективы
развития транспорта на севере России. 2015. №1. С.32-34.

5.
Синицын С.А. Формализация погрешностей в задачах оптимизации геометрических
моделей// Инновации и инвестиции. 2018. № 11. С. 175-180.

6.Левчук
Т.В., Ким А.Р. Трехмерное моделирование при визуализации математических и
технических задач// История и перспективы развития транспорта на севере России.
2016. №1. С.75-78.

7.Левчук
Т.В., Втулкин М.Ю., Череватый Д.Н. Применение интегрированных пакетов в частных
задачах вычислительной математики //История и перспективы развития транспорта
на севере России. 2014. №1. С.199-200.

8.Левчук
Т.В., Втулкин М.Ю. Инновационные технологии на железнодорожном транспорте//
История и перспективы развития транспорта на севере России. 2012. №1. С.68-71.

Другие новости

Авторы

Идрисова Ольга Сергеевна

18 мая

Авторы

Матвеева Марина Станиславовна

18 мая

Авторы

Шодиев Манучехр Бахромович

18 мая

Авторы

Смагулова Гульжихан Советбековна

18 мая