Рассмотрим следующую ситуацию. Пусть в некоторой экологической системе возник очаг нового вида организма, обладающего лучшей приспособленностью к условиям данной среды. Предположим, что вследствие активности среды особи данного вида начинают немедленно размножаться во всех ее точках сразу после возникновения. Размножение организмов возможно и за очагом размножения, куда они проникают в результате диффузии. В силу экологических, экономических и некоторых других потребностей возникает необходимость определения размера популяции в заданной точке среды в любой момент времени процесса.
Как известно, одномерное уравнение Фишера
(1)
с безразмерным параметром a > 0, в котором искомая функция u = u(x,t) представляет плотность популяции, 0 ≤ u ≤ 1, является формализованным описанием данного процесса, т.е. представляет собой простейшую математическую модель динамики популяции.
Пусть плотность популяции во всех точках активной среды в момент возникновения нового типа организма, т.е. в момент времени t = 0, задается функцией φ(x), а ее изменение на границах среды x = 0 и x = l за все время процесса определяется через функции ψ1(t) и ψ2(t). Математическая формализация приводит к задаче нахождения интегрируемой функции 
, удовлетворяющей уравнению (1) в области Q = {(x, t): 0 < x < l, 0 < t < T}, а также следующим начальным и граничным условиям при 
(2)
Для построения визуальной модели динамики популяции редуцируем уравнение (1) к следующему нагруженному уравнению:
(3)
Согласно принятой терминологии точное или приближенное решение задачи (3), (2) будем считать приближенным решением задачи (1), (2).
Для дальнейших рассуждений необходима априорная оценка решения задачи (3), (2), полученная в [1]:
(4)
Здесь постоянная C зависит только от t и l. Выберем ее таким образом, чтобы в (4) выполнялось строгое равенство, и перейдем от (3) к уравнению
(5)
Таким образом, произведена линеаризация исходного нелинейного уравнения (1), путем его редукции к нагруженному уравнению (3) и последующему переходу к линейному уравнению (5).
Решение задачи (5), (2) определяется с помощью функции Грина G(x,x,t) для параболического уравнения c правой частью F(x, t):
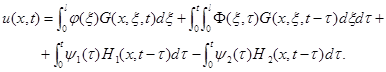(6)
Пример. Пусть φ(x) = lx – x2 + 0,5, а ψ1(t) = ψ2(t) = 0,5, что соответствует половинной возможной численности популяции на границах среды за все время расчета. Пусть l = 1, тогда можно положить F(x, t) = –a2. Вычислим интегралы в (6) ограничиваясь первыми членами разложений входящих сюда функций. Найденную функцию обозначим через u(0):
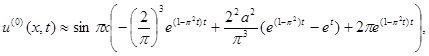(7)
и будем считаться решением задачи (1), (2) в начальном приближении. Это решение можно “улучшить” путем реализации следующего итерационного процесса [2].
1. При k = 1 решить задачу (2) для уравнения (1), записанного в виде
(8)
2. Полагая k = k + 1 подставить найденную функцию u(k) в правую часть итерационного уравнения (3) и найти очередное “уточненное” решение u(k+1).
Процесс завершить при реализации желаемого количества итераций или при достижении заданной точности вычислений.
Применение этого процесса со стартовой функцией (7) дает формулу общего члена последовательности приближенных решений задачи (1), (2):
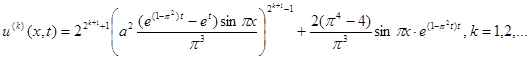(9)
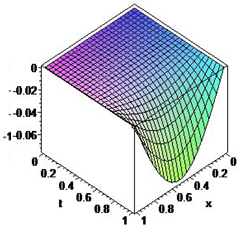
Получено аналитическое выражение, позволяющее последовательно аппроксимировать решение задачи (1), (2) функциями u(k)(x, t), т.е. определять плотность популяции в любой точке среды в требуемый момент наблюдения. На рисунках ниже приведены поверхности u(k)(x,t), k = 0,1,2,3, полученные по формуле (9) в системе компьютерной математики Maple.
u(0)(x,t) u(1)(x,t)
 |
 |
||
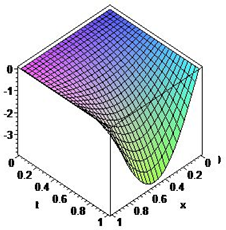u(2)(x,t) u(3)(x,t)
Эти поверхности являются моделями динамики популяции различной точности. Рисунки позволяют визуально отслеживать изменение популяции в различных точках среды. Точное значение размера популяции в выбранной точке можно найти по формуле (9).
Таким образом, редукция к нагруженному уравнению позволяет моделировать динамику популяции путем нахождения в аналитическом виде приближенного решения поставленной задачи. Предполагается, что предлагаемый способ может быть эффективным для визуального и имитационного моделирования различных биологических и экологических систем.
Использованные источники
1. Об аппроксимации решения однородного параболического уравнения со степенной нелинейностью решением ассоциированного нагруженного уравнения // Сборник трудов международной научной конференции «Современные проблемы прикладной математики, информатики и механики». 10-14 июня 2019 г. ЭУНК КБГУ, п. Эльбрус, КБР. Нальчик: Изд-во КБГУ. Т. 2., 2019. – 193 с. С. 37 – 44 .
2. Бозиев О.Л. Применение нагруженных уравнений к приближенному решению дифференциальных уравнений в частных производных со степенной нелинейностью // Вестник Тверского государственного университета. Серия «Прикладная математика». 2015, № 1. С. 127 – 136.
