Теорема Менелая (прямая): «Если
на сторонах AB и BC треугольника ABC взяты соответственно точки ![]() и
и ![]() ,а
,а
точка ![]() взята
взята
на продолжении стороны AC за точку C (рис.1), то точки ![]() ,
, ![]() и
и ![]() лежат
лежат
на одной прямой тогда и только тогда,когда выполнено равенство
![]()
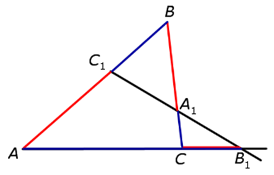
Рис.1
Теорема Менелая (обратная): «Если
на продолжениях сторон AB, BC и AC треугольника ABC взяты соответственно точки ![]() ,
,![]() и
и ![]() ,то
,то
точки ![]() ,
,![]() и
и ![]() лежат
лежат
на одной прямой тогда и только тогда,когда выполнено равенство
![]()
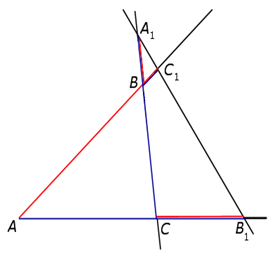
Рис.2
Задача: Точки ![]() и
и ![]() лежат на сторонах соответственно AC и AB треугольника ABC, причем
лежат на сторонах соответственно AC и AB треугольника ABC, причем ![]() . Прямые
. Прямые ![]() и
и ![]() пересекаются в точке O.
пересекаются в точке O.
а) Докажите, что прямая AO делит пополам сторону BC.
б) Найдите отношение площади
четырехугольника ![]() к площади
к площади
треугольника ![]() ,если известно, что
,если известно, что ![]()
![]()
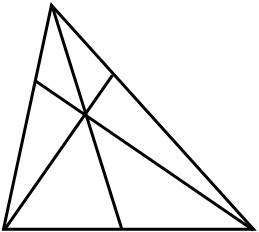

Решение: а) По теореме Менелая
имеем:
в ![]() :
: ,а в
,а в  .Т.к.
.Т.к. 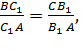 то
то 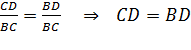 ,ч.т.д.
,ч.т.д.
б) По теореме Менелая имеем:

Так как у треугольников ![]() общая высота
общая высота ![]() ,то
,то 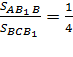 . Следовательно,
. Следовательно,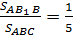 .
.
Аналогично доказываем, что 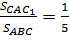 .Треугольники
.Треугольники ![]() имеют общую высоту
имеют общую высоту ![]() , поэтому
, поэтому 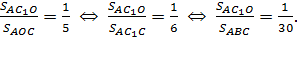
Аналогично доказываем, что 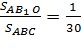 . Следовательно,
. Следовательно, 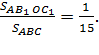
Ответ:1:15
Задача: ABCD-четырехугольник.
М-середина AD. N-середина BC.MP=PK=KN. Доказать: ABCD-трапеция;DC=2AB.
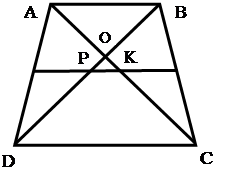
Решение: Используем теорему
поочередно к треугольникам:
![]() и секущая DO (точки пересечения O,P,D):
и секущая DO (точки пересечения O,P,D): . Следовательно,
. Следовательно, ![]()
![]() и секущая OC (точки пересечения O,K,C):
и секущая OC (точки пересечения O,K,C): .Следовательно,
.Следовательно,![]()
![]() и секущая AK (точки пересечения M,P,K):
и секущая AK (точки пересечения M,P,K): . Следовательно,
. Следовательно,![]()
![]() и секущая PN (точки пересечения P,K,N):
и секущая PN (точки пересечения P,K,N): . Следовательно,
. Следовательно,![]()
Значит, DO=4PO; BO=2PO, т.е. 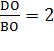
CO=4OK; AO=2OK, т.е. 
В 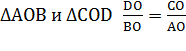 ,
, ![]() вертикальные, следовательно,
вертикальные, следовательно, ![]() , следовательно,
, следовательно,![]() (накрест лежащие при прямых AB и DC и секущей AC), следовательно,
(накрест лежащие при прямых AB и DC и секущей AC), следовательно, ![]() Значит, ABCD-трапеция.
Значит, ABCD-трапеция.
Из равенств 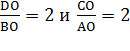 видно, что стороны подобных треугольников
видно, что стороны подобных треугольников
![]() и
и ![]() относятся как
относятся как ![]() , значит,
, значит, 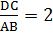 и DC=2AB, ч.т.д.
и DC=2AB, ч.т.д.
Список использованной литературы.
1. Атанасян
Л.С. и др. Геометрия. 7 – 9 класс. – М.: Просвещение, 2018.
2. Зетель
С.И. Новая геометрия треугольника. Гос. уч. – пед. изд-во, М.: 1962.
3. Шарыгин
И.Ф. Геометрия. Задачник.9—11 классы. — М.: Дрофа, 1996.

