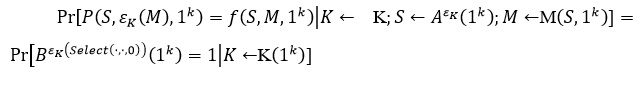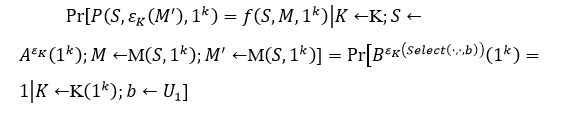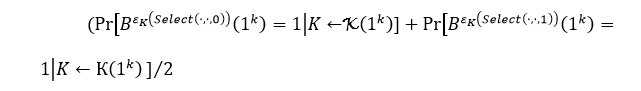Безопасность криптосистем с открытым ключом обычно классифицируется с точки зрения их целей и моделей атак. Стандартные цели криптосистем с открытым ключом заключаются в следующем.
- a) Семантическая безопасность (SEM): в этом понятии безопасности любой злоумышленник (вероятностная машина Тьюринга за полиномиальное время) не может получить какую-либо частичную информацию о незашифрованном тексте данного зашифрованного текста. Это понятие соответствует вычислительной версии «совершенной секретности», введенной Шенноном. [1]
- b) Неразличимость (IND): здесь, учитывая зашифрованный текст одного из двух открытых текстов, любой злоумышленник не может отличить, какой из них зашифрован. Это понятие довольно искусственное, но при рассмотрении доказуемой безопасности криптосистемы с открытым ключом обычно удобно использовать это понятие в качестве цели системы [2].
- c) Недопустимость (NM): учитывая зашифрованный текст открытого текста, любой противник не может создать другой зашифрованный текст, открытый текст которого по смыслу связан с исходным [3].
В статье рассматривается эквивалентность понятий семантической безопасности (SEM) и неразличимости (IND).
Эквивалентность семантической безопасности и неразличимости
Доказательство эквивалентности семантической безопасности и неразличимости сводится к тому, что необходимо доказать, что схема симметричного шифрования (K, ε, D) защищена SEM-CPA тогда и только тогда, когда это последний вызов IND-CPA.
Для этого предположим, что система защищена SEM -CPA. Пусть B будет любой парой оракула PPT и определена как
Покажем, что e(K) незначительно. Пусть A на входе 
имитирует B на входе, пока B не выдаст пару запросов, содержащих отдельные элементы. (До этого момента B делал только пару запросов с тем же аргументом, чтобы A мог имитировать их с помощью вызова своего оракула.) А затем выводит все содержимое памяти В в этой точке, включая пару (М0, М1) различных запросов. Определим М 
как распределение, которое выбирает каждый из М0 или М1 с вероятностью 1/2. Определим 
= 1 и пусть P моделирует остаток вычисления B, начиная с памяти S, используя возвращенный зашифрованный текст C из парного оракула.
Соблюдая это
а также
Согласно SEM-CPA эти две величины в какой-то степени незначительны 
относительно друг от друга. Последнее количество просто
Для заданных f, A, P и M определим пару оракулов PPT B, которая на входе имитирует A на входе и вызывает своего оракула с (Mi, Mi) всякий раз, когда A вызывает своего оракула с помощью Mi, пока A не выдаст S. Затем B вызывает M на входе S и дважды, чтобы получить M и M’. Он вызывает своего парного оракула в паре (M, M’), дающего некоторый C, проверяет, если P (S, C, ) = f (S, M,), выдает 1, если они равны, и 0, если они не равны.
Теперь
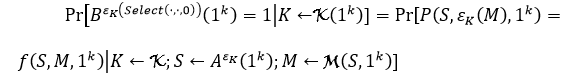и, таким образом, безопасность IND-CPA подразумевает, что эти две величины находятся в пределах некоторого незначительного значения друг от друга, что подразумевает безопасность SEM -CPA.
Результаты
В проделанной работе сформулированы основные цели криптосистем, а также описано доказательство эквивалентности семантической безопасности (SEM) и неразличимости (IND).
Заключение
Рассмотренное в статье доказательство эквивалентности семантической безопасности (SEM) и неразличимости (IND) позволяет анализировать безопастность криптосистемы путём исследования только одного из этих свойств. Таким образом, доказав безопасность криптосистемы по одному свойству, автоматически доказывается безопасность системы по второму свойству.
Список литературы
- Watanabe Y., Shikata J., Imai H. Equivalence between semantic security and indistinguishability against chosen ciphertext attacks //International Workshop on Public Key Cryptography. – Springer, Berlin, Heidelberg, 2003. – С. 71-84.
- Gagliardoni T., Hülsing A., Schaffner C. Semantic security and indistinguishability in the quantum world //Annual Cryptology Conference. – Springer, Berlin, Heidelberg, 2016. – С. 60-89.
- Beame P. Cryptography: lections. URL:
https://courses.cs.washington.edu/courses/cse599b/06wi/ .
