Данный
курс будет полезен школьникам для более глубокого понимания школьной программы
по геометрии и расширению кругозора. Студентам математических дисциплин
педагогических ВУЗов его можно рассматривать, как базу для проведения
спецкурса, основу для написания дипломных и курсовых работ.
Перед
тем, как приступить непосредственно к заявленной теме, напомним необходимые
фундаментальные понятия.
История
возникновения геометрии Лобачевского.
По
официальной версии в III
веке до н. э. древнегреческим математиком Евклидом была формализована
геометрия. Из предложенной Евклидом аксиоматики выделялся пятый постулат,
который утверждал, что из любой точки, не лежащей на заданной прямой, можно
провести единственную параллельную ей прямую. На протяжении многих веков
математики пытались вывести данное утверждение из других аксиом. Точку в этом
вопросе поставил русский математик Лобачевский (1792 – 1856). Лобачевский
поменял пятый постулат на его отрицание: через точку, не лежащую на прямой,
проходит более чем одна прямая, не пересекающая данную. Он доказал, что данное
утверждение не противоречит остальным аксиомам, а в совокупности с ними
образует другую геометрию.
Инверсия
В
дальнейшем мы будем часто использовать инверсию – преобразование плоскости.
Инверсия производится относительно фиксированной окружности. Правило, по
которому точки плоскости переходят друг в друга, поясняет рисунок 1.
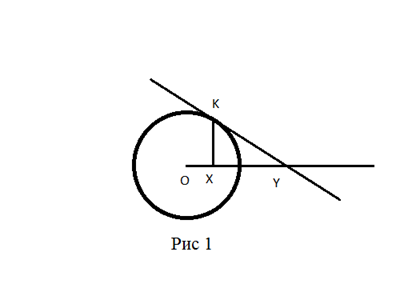
Т.е.
чтобы найти Y – образ лежащей внутри
окружности точки X,
нужно из точки X восстановить
перпендикуляр к ОХ до пересечения с окружностью (точка K),
точку Y получаем как пересечение
касательной в точке K
и OX. А чтобы найти точку X
– образ лежащей вне окружности точки Y,
нужно из Y провести касательную и
из точки касания опустить перпендикуляр на OY.
Отметим,
что при инверсии
– точки, лежащие вне
окружности, переходят в точки внутри окружности и наоборот,
– точки, лежащие на
окружности, остаются неподвижными,
– центр окружности не
имеет образа (условно считаем, что образ O
– бесконечная точка).
При
инверсии прямые, проходящие через O,
переходят сами в себя. Остальные прямые, переходят в окружности, проходящие
через O (в точку O
переходят бесконечно удаленные точки прямой) и наоборот. Остальные окружности
(не проходящие через центр) переходят в окружности. На рисунке ниже приведены
примеры образов окружностей и прямых при инверсии.
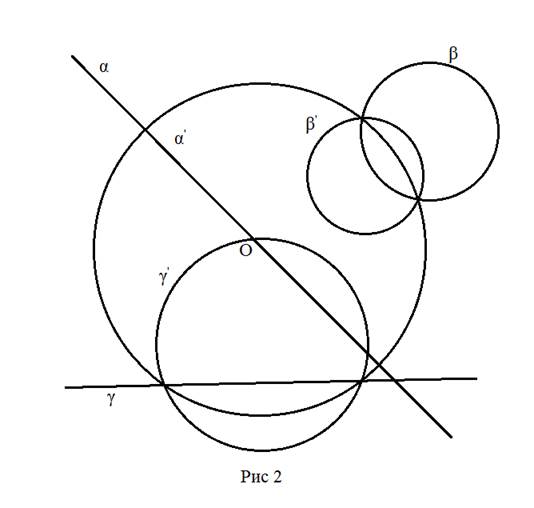
Важным
свойством инверсии является конформность – сохранение углов между прямыми и
другими линиями (нас будут интересовать только прямые и окружности). При
инверсии окружность переходит сама в себя тогда и только тогда, когда
окружность перпендикулярна окружности, относительно которой производится преобразование
инверсии. Если окружности α и β перпендикулярны то как
окружность β переходит в себя при инверсии относительно α,
так и α переходит в себя при инверсии относительно β. Легко
доказать следующее утверждение:
Если
окружности α и β пересекаются в двух точках и, при
инверсии относительно окружности α, на β найдется
точка, образ которой также лежит на β, то и вся окружность β
перейдет сама в себя.

Действительно,
по условию все четыре точки X,
Y, A,
B лежат на β.
Образ окружности β проходит через точки A,
B (остаются неподвижными)
и Y (образ точки X).
Т.е. β и ее образ совпадают, т.к. проходят через три
одинаковые точки.
Модель
Пуанкаре плоскости Лобачевского.
Произвольную
окружность на плоскости назовем Абсолютом. В круге, ограниченном Абсолютом,
реализуется геометрия Лобачевского, если в качестве прямых выбрать окружности,
перпендикулярные Абсолюту.
На
рисунке ниже проиллюстрированы все возможные расположения двух прямых. А
именно, они могут пересекаться в точке (например γ и β),
быть параллельными (α и δ), т.е. стремиться к общей
точке на Абсолюте (для α и δ это точка A),
и быть расходящимися (т.е. не имеют общих точек, в том числе и на Абсолюте). В
последнем случае, прямые α и β имеют единственный общий
перпендикуляр – прямую γ.
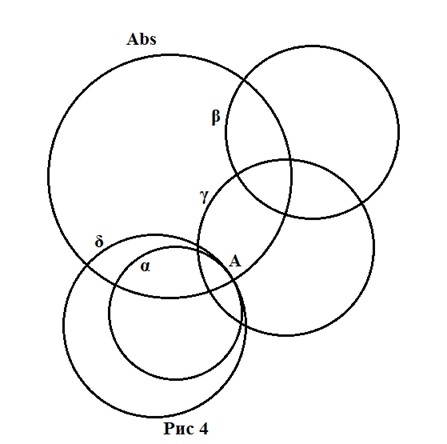
Поясним
на примере, как воспринимать ограниченность модели плоскости Лобачевского.
Действительно, когда мы рассматриваем обычную (Евклидову) прямую,
предполагается, что она бесконечна, а модель Пункаре всю плоскость Лобачевского
размещает в ограниченный круг. Для понимания этого явления рассмотрим любой
отрезок OY. Если измерить его длину
обычным способом (например, линейкой), она будет иметь конкретную, конечную
величину. Но если установить соответствие точек на отрезке OY
и
точек на луче OX, как показано на
рисунке ниже, и рассматривать расстояние между точками A,
B, как расстояние между их
образами A‘ и
B‘
этих точек на луче OX,
получаем, что при приближении к концу отрезка Y,
расстояние стремится к бесконечности.
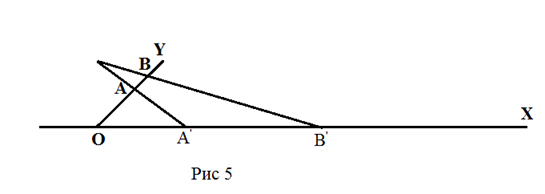
Т.е. так же, как точка Y
на отрезке соответствует бесконечно удаленной точке, так и все точки, лежащие
на Абсолюте, соответствуют бесконечно удаленным точкам плоскости Лобачевского.
Как
отмечалось выше, все окружности, перпендикулярные Абсолюту, изображают прямые.
Поставим вопрос, что изображают остальные окружности.
Прежде
всего, отметим, что любые окружности плоскости Лобачевского изображаются
конечными (т.е. не имеющими общих точек с Абсолютом) окружностями в модели
Пуанкаре.
Рассмотрим
некоторую прямую, уходящую на Абсолют в точки A
и
B. Тогда любая другая окружность,
проходящая через точки A
и
B, изображает эквидистанту к выбранной
прямой. Эквидистантой называется линия, все точки которой удалены от
фиксированной прямой на одинаковое расстояние в одну сторону. Если в евклидовой
плоскости, каждую точку некоторой фиксированной прямой, сдвинуть на
фиксированное расстояние, получится другая прямая, параллельная исходной. В
плоскости Лобачевского, при данной процедуре, получается эквидистанта – не
прямая, а некоторая изогнутая линия. Экидистанта это что то среднее между
евклидовой прямой и евклидовой окружностью – как прямая она бесконечна и, как
окружность, равномерно загибается в каждой своей точке.

Пограничным
случаем между эквидистантой и окружностью является орицикл. Орицикл
изображается окружностью, касающейся Абсолюта в одной точке. Т.е. орицикл,
также как эквидистанта и окружность, равномерно загибается в каждой своей
точке. Если изгиб станет чуть меньше, орицикл превратится в эквидистанту, а
точка касания Абсолюта превратится в две различные точки, а если чуть больше,
орицикл превратится в окружность, а точка касания «оторвется» от Абсолюта
(окружности не имеют общих точек с Абсолютом).
Как
и в евклидовой плоскости, в плоскости Лобачевского, все точки равны между
собой. За начало координат в евклидовой плоскости можно взять любую точку.
Аналогично, в плоскости Лобачевского за центр модели можно выбрать произвольную
точку. Но вот изображением прямых, проходящие через центр модели, являются
только прямые (в смысле евклидовой плоскости). В то время как прямые,
проходящие через другие точки, изображаются окружностями.
Элементарные
построения на плоскости Лобачевского.
Выше
была дана необходимая информация о плоскости Лобачевского. Переходим
непосредственно к решению задач. Все построения будут проводиться в модели
Пункаре, т. е. в круге с центром O,
ограниченном окружностью Abs.
Задача
1.
Построить прямую, проходящую через две заданные точки.
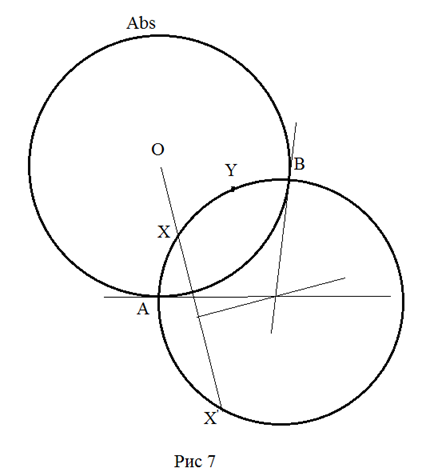
Решение.
То есть, нужно построить окружность, проходящую через заданные точки X
и
Y, перпендикулярную окружности Abs.
Достаточно построить образ X‘ точки
X при инверсии относительно окружности
Abs и провести окружность
через точки X,
Y и X‘.
В качестве точек X,
Y можно было взять и точки
на Абсолюте – A,
B. В этом случае, центр
искомой окружности можно найти, как пересечение касательных к Abs
в точках A и
B. Или можно взять одну конечную точку
(точка X) и одну точку на
Абсолюте (точка B). Тогда, центр
искомой окружности, изображающей прямую в плоскости Лобачевского, находится как
пересечение касательной в точке B
и серединного перпендикуляра к отрезку XX‘.
Из
реализации построения следует, что существует единственная прямая, проходящая
через две различные заданные точки.
Задача
2.
Через заданную точку провести прямую в заданном направлении.
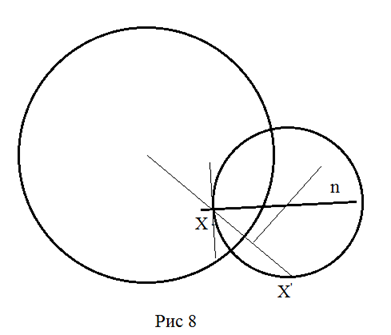
Решение.
Центр искомой окружности находим как пересечение серединного перпендикуляра к
отрезку XX‘
и прямой n, проходящей через точку X
и перпендикулярной заданному направлению. Такая прямая (в смысле плоскости
Лобачевского) единственна.
Задача
3.
Из заданной точки провести перпендикуляр к заданной окружность.
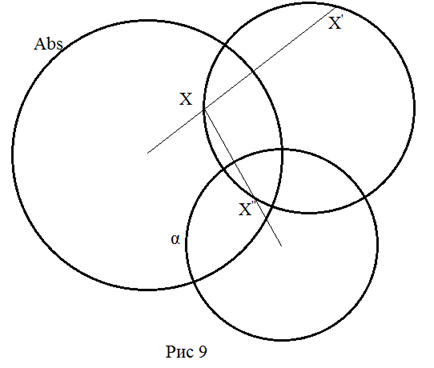
Решение.
Искомая прямая изображается окружностью, проходящей через точки X,
X‘ и
X”,
где X‘
образ точки X при инверсии
относительно окружности Abs,
а X” образ
точки X при инверсии
относительно окружности α, изображающей заданную прямую.
Отметим,
что мы также научились строить точку, симметричную данной, относительно
заданной прямой (это точка X”).
Если
окажется, что заданная точка X
лежит на заданной прямой, то имеется направление – перпендикуляр к α,
в котором должна проходить искомая прямая. Поэтому для решения достаточно
воспользоваться задачей 2.
Задача
4.
Построить серединный перпендикуляр к заданному отрезку. Найти середину отрезка.
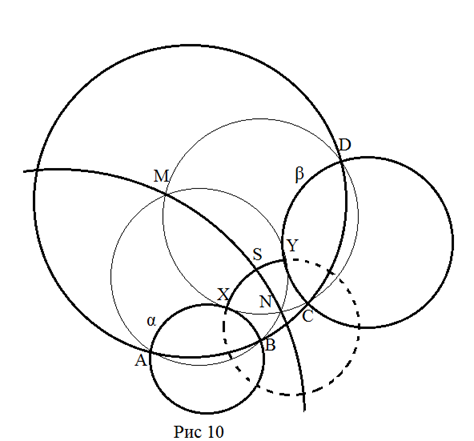
Решение.
Через концы заданного отрезка XY
проведем прямые α и β, перпендикулярные этому отрезку (задача
2). Пусть A, B
и C, D
точки пересечения этих окружностей с Абсолютом. Окружности α‘
и β‘, проходящие через точки A,
B, Y
и
C, D,
X соответственно,
изображают эквидистанты к прямым α и β. Точки их
пересечения – N и
M равноудалены
от прямых α и β на расстояние, равное длине их общего
перпендикуляра. Прямая, проходящая через точки N
и
M, является искомым перпендикуляром, а
точка S –
пересечение заданного отрезка и NM
– серединой отрезка.
Задача
5.
Построить общий перпендикуляр двух заданных прямых.
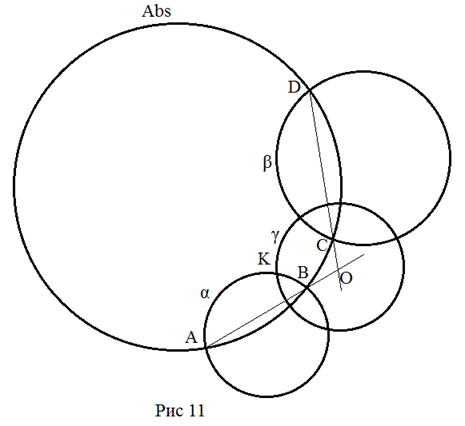
Решение.
Пусть α и β заданные прямые и A,
B, C
и D точки этих прямых на
Абсолюте. Пусть O – точка
пересечения прямых AB
и
CD. Из O
проведем касательную OK
(K
– точка касания) к α. Проведем окружность γ с центром O
и
радиусом OK. Покажем, что γ
изображает искомую прямую. Нужно доказать, что γ прямая (т.е.
перпендикулярна Abs) и
перпендикулярна к α и β.
По
построению γ перпендикулярна α. При инверсии
относительно γ точка A
переходит
в B. Поэтому Abs
и
γ перпендикулярны. Значит, γ изображает окружность и
осталось показать, что γ и β тоже перпендикулярны. Abs
и
γ перпендикулярны, поэтому при инверсии относительно γ,
точки C и
D переходят друг в друга и,
следовательно, окружности α и γ перпендикулярны.
Задача
6.
Построить центр заданной окружности.
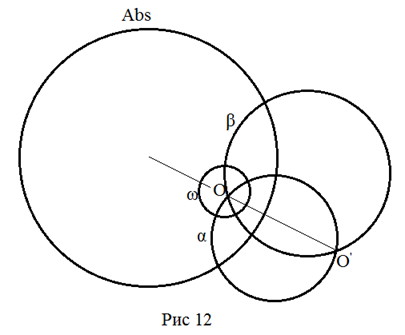
На
заданной окружности ω возьмем две произвольные точки и проведем из
них прямые α и β, перпендикулярные заданной окружности.
Точка O –
точка пересечения этих прямых, является искомой.
Чтобы
обосновать последнее утверждение, докажем, что любая прямая, проходящая через O,
также перпендикулярна ω.
Пусть
O‘ –
образ точки O при инверсии
относительно Abs. Тогда α
и β проходят через O‘,
т.к. они прямые и переходят сами в себя при этой инверсии. Рассмотрим теперь
инверсию относительно ω. Прямые α и β также
переходят сами в себя (т.к. перпендикулярны ω по построению).
Значит, точка O переходит в точку
O‘ и
при инверсии относительно ω. Поэтому любая прямая, проходящая через
точку O, проходит и через точку O‘
(т.к. она прямая) и, следовательно, перпендикулярна окружности ω.
Обращаем
внимание на то, что O
не совпадает с центром окружности ω, изображающей окружность в
плоскости Лобачевского. Изображение центра не совпадает с центром изображения.
Задача
7.
Построить окружность с центром в конце заданного отрезка и радиусом равным
этому отрезку.

Пусть
OX – заданный отрезок. Проведем через O
две произвольные прямые и построим точки X‘ и
X”
– точки симметричные X
относительно этих прямых. Окружность, проходящая через точки X,
X‘ и
X”,
является искомой.
Задача
8.
От заданной точки на заданной прямой отложить заданный отрезок.
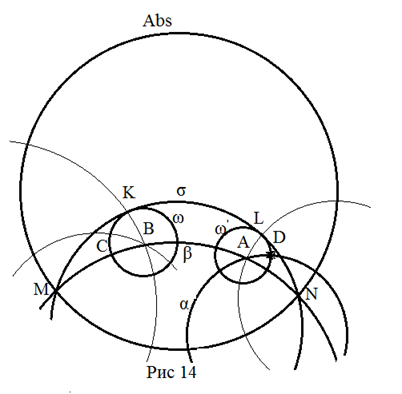
Пусть
заданная точка A лежит на прямой α.
И пусть BC – заданный отрезок. Через
точки A и B
проведем прямую β. Обозначим через N
и
M точки пересечения β и Abs.
Построим окружность ω с центром в точке B
и радиусом BC. Из точки B
восстановим перпендикуляр к β до пересечения с ω в
точке K. Через точки N,
M и K
проведем эквидистанту σ. Из точки A
восстановим перпендикуляр к β до пересечения с σ в
точке L. Наконец, проведем
окружность ω‘ с центром в A
и радиусом AL. Точка D
– пересечение окружности ω‘и прямой α. По
построению AD = AL
= BK = BC,
поэтому точка D – искомая.
Рассмотренные
выше задачи являются базовым инструментом для построения на плоскости
Лобачевского. Используя этот инструмент можно решать широкий круг более сложных
задач. Для примера рассмотрим следующую задачу.
Задача
9.
Построить прямоугольный треугольник по катету и прилежащему к этому катету
углу.
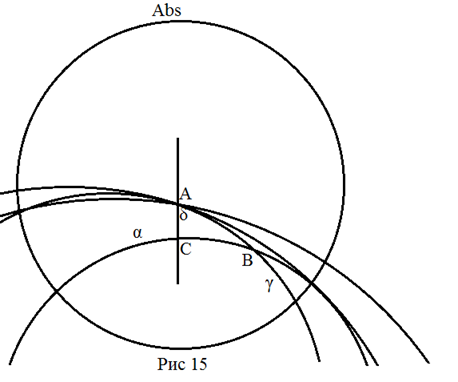
Решение.
На прямой α отметим точку C.
Из точки C восстановим
перпендикуляр к α и отложим на нем отрезок CA,
равный заданному катету. В точке A
от прямой CA отложим заданный угол δ
и проведем прямую γ в полученном направлении. Точка B
– точка пересечения γ и α является третьей точкой
треугольника.
Исследование.
Из построения видно, что при маленьких δ, решение существует. А вот
при больших δ прямые γ и α будут
расходящимися и не имеют точек пересечения. Т.е. треугольника не существует.
Отметим
пограничный случай, когда γ и α параллельны. В этом
случае величина угла δ имеет конкретное значение, зависящее только
от длины отрезка CA. Такой угол
называется углом параллельности. Чем меньше CA,
тем ближе δ приближается к прямому углу. Чем больше CA,
тем меньше δ и, при стремлении CA
к бесконечности, δ стремится к 0.
Литература
1. Жафяров А.Ж., Бурова
Н.А., Шрайнер Е.Г., Щербаков А.А. Векторы на плоскости и в пространстве//
учебно-дидактический комплекс / Новосибирск, 1993.
2. Щербаков А.А. Выпуклые
гиперповерхности с заданной условной кривизной в гиперболическом пространстве//
автореферат диссертации на соискание ученой степени кандидата
физико-математических наук / Институт математики СО РАН СССР. Новосибирск, 1991.
3. Щербаков А.А.
Элементарные построения на плоскости Лобачевского// научный электронный журнал
Меридиан. 2020. № 9(43). С. 207-209.

