Частный случай неравномерной статистики
ошибок, причиной которого
является перекрытие слотов передачи
соседних импульсов, в наиболее популярных форматах модуляции сводится к
большому количеству ошибок при передаче триплета 101. Такое положение вещей
характерно для формата амплитудной модуляции сигнала (или формата ООК, on-off
keying), а также для фазовых форматов BPSK и DBPSK. Разумеется, что изменение
способа формирования сигнала может привести к ситуации, при которой, например,
самый «неблагонадёжный» паттерн будет не 101, а «обратный» ему 010, однако
при общепринятом формировании импульсов
наиболее подвержен ошибкам
при передаче данных с перекрытием соседних
слотов именно триплет 101.В силу этого рассмотрение ограниченных кодов имеет
смысл начать с данного
частного случая, а именно случая
уменьшения количества триплетов 101 в передаваемом сообщении, впоследствии
обобщив его на общий случай неравномерной статистики ошибок, охватывающий все
возможные асимметрии
канальных искажений.
Прежде чем предложить и
проанализировать способы построения кода, удаляющего битовые сочетания 101 из
сообщения, заметим, что стандартный код RLL (2, +∞) пригоден для этой
цели и удаляет из сообщения абсолютно все сочетания 101, поскольку ограничивает
снизу количество нулевых битов, следующих между последовательными «единицами» —
для данного кода между двумя «единицами» будет по меньшей мере два «нуля», что,
очевидно, избавляет сообщение от 101. Таким образом, поставленная задача
решается известными ещё с 1970-х годов методами, однако данное решение не
оптимально в том смысле, что максимальная кодовая скорость кода D = (2,
+∞), его ёмкость, равна C(D) = 0.5515, то есть любой
практически реализуемый код будет иметь кодовую скорость, не превосходящую C(D).
Это означает, что избыточность такого кода будет по меньшей мере около 45%.
Причиной столь высокой избыточности кода RLL является то обстоятельство, что
помимо удаления 101 данный код удаляет и ряд других паттернов, которые никак не
связаны с решением поставленной задачи. Ниже будет показано, что задачу
возможно решить с помощью кода с избыточностью в 20%, что существенно
эффективнее RLL-кодов.
Помимо большой
избыточности кодов RLL, есть ещё один
очень важный
аспект, в силу которого разработка
альтернативных методов ограниченного кодирования является актуальной. Это
необходимость гибкости в применении подобных кодов, поскольку радикальное
решение, предлагаемое RLL и заключающееся в
полном устранении 101 из сообщения, далеко не всегда является необходимостью,
так как иногда достаточно лишь частично ограничить количество «проблемных»
битовых сочетаний. Поскольку во всякой коммуникационной системе для надёжного
обнаружения и коррекции ошибок применяются помехоустойчивые коды, то коды с
ограничениями имеет смысл применять в качестве дополнения к корректирующим
кодам с целью снижения ошибок до уровня, на котором уверенно работает схема
коррекции ошибок.
Эффект от сочетания кодов
достигается за счет снижения фактической частоты ошибок в канале благодаря
ограниченному коду с одной стороны и за счёт использования корректирующих
свойств помехоустойчивого кода с другой стороны, который при отсутствии
ограниченного кода работает неэффективно из-за большого количества ошибок в
канале. Именно в этом контексте задача разработки кода с возможностью
управления степенью удаления того или иного паттерна обретает не только
теоретическое, но и практическое значение.
Прежде всего
рассмотрим простой способ удаления битового сочетания 101, который может быть
реализован как в потоковом, так и в блочном исполнении, если длину потока
ограничить сверху. Теоретические аспекты кодирования, на котором основан
алгоритм, изложены в [2, 3]. Основным параметром кода является величина ![]() ,
,
принимающая значения 0 < ![]() <
<
1. В качественном отношении данный параметр имеет следующий смысл: если N101—
количество триплетов 101 до кодирования, a ![]() —
—
количество триплетов после декодирования, то ![]() .
.
В частности, ![]() =
=
1, если сообщение лишается всех триплетов 101 (![]() =
=
0), и ![]() =
=
0, если сообщение не подвергается кодированию. В последующих разделах работы
обозначение ε будет использовано в схожем качественном смысле, но для
других кодов.
Обозначим за bi i-й
бит в исходном сообщении, а за Тi=
bibi+1bi+2
обозначим i-й триплет сообщения
(предполагается, что передача потока ведётся от младших битов к старшим,
поэтому в данном обозначении Тi
представляет собой двоичное число, старший бит которого равен bi+2,
средний — bi+1
, а младший — bi).
Самый простой способ удалить триплет
Тi = 101 заключается в
замене данного триплета на 100, с последующей вставкой единичного бита, который
будет сигнализировать о том, что предыдущий триплет был не 100, а 101. Таким
образом, кодирование порождает следующие замены в обрабатываемом потоке данных:
101
![]() 1001
1001
100![]() 1000.
1000.
Таким образом, данный подход есть не
что иное, как частный случай битовой
вставки (bit stuffing)
— метода кодирования, который уже был упомянут как метод, применяемый в
технологии USB. Также с помощью этого
метода, например, могут быть построены коды RLL
с различными параметрами. В данном случае каждый триплет сообщения принимается
без изменений, однако если он равен 100, то следующий за ним бит показывает,
что именно на самом деле было передано — 101 или 100. Совокупность
дополнительных битов образует избыточность кода, величина которой будет
определена ниже.
Преимуществом
данного подхода является его простота, поскольку для кодирования фактически
достаточно проанализировать текущий передаваемый триплет: если он равен 100, то
добавить 0, если он равен 101, то либо ничего не менять, либо вставить
дополнительный «нуль» между единичными битами. Однако данный подход несёт в
себе существенный недостаток, впрочем, являющийся общим местом для кодов с
ограничениями, обрабатывающих как единое целое длинные кодовые слова. Если
сообщение представить длинным потоком и с помощью битовой вставки убрать часть
«опасных» триплетов, то обработка последних битов потока на приёме находится в
строгой зависимости от обработки первых битов потока, поскольку если происходит
ошибка в триплете 100, то кодовая схема теряет ориентир, по которому она
распознаёт, была битовая вставка в 101 или её не было.
Тем не менее, при
разбиении сообщения на блоки небольшой длины такой подход на практике оправдан,
поскольку позволяет локализовать возможные ошибки, возникшие при передаче
сообщения. Тем самым потоковый код становится кодом потоково-блочным. Размер
блока в этом случае определяется исходя из свойств канала передачи данных и
вероятности ошибки передачи. Если же вдобавок к каждому блоку добавлять
некоторую информацию, по которой можно судить о верности передачи (например,
контрольную сумму или биты четности, или количество триплетов 100 в нём), то
это позволяет минимизировать вероятность возникновения проблем с
синхронизацией.
Пусть даны
натуральные числа р, q, q < р. Представим
исходное сообщение в виде массива триплетов Тi.
Наша задача состоит в преобразовании сообщения таким образом, чтобы в преобразованном
сообщении отсутствовали (полностью или частично) триплеты 101. Рассмотрим
формирование блока данных, однако сначала договоримся за rk
обозначать k-й бит в результирующем
блоке данных (0 ≤ k ≤
n,
где n
— размер результирующего блока данных), за Rk = rk rk+1
rk+2
обозначим к-й паттерн блока-результата, а за j будем обозначать
количество триплетов 100 в результирующем блоке (по мере кодирования j будет
расти).
Кодирование
сообщения будет происходить последовательно, бит за битом, по следующей схеме:
если Тi
≠ 100 и Тi
≠ 101, Rk = Тi
(изменений не вносится). Если Тi
= 101 и (j mod р) < q, то Rk = 1001;
в случае, если
(j mod р) > q, то удаления триплета не происходит и Rk
= 101. Если Тi
= 100, то возможны два случая: когда (j mod р) > q, то Rk
— 1000, где последний нулевой бит сообщает о том, что исходный триплет был
именно 100, а не 101; в случае, когда (j mod р) > q, Rk
= 100.
Такой подход, как
будет показано ниже, имеет ряд преимуществ, одним
из которых является точное
выдерживание заданного значения е, которое выражается через р и q с помощью
довольно простого соотношения. Однако для начала приведём законченную
последовательность действий, необходимых для реализации кода.
Поскольку при
кодировании отдельного рассмотрения требуют лишь триплеты 001 и 101, назовем их
особыми триплетами, так как остальные триплеты копируются из исходного
сообщения в закодированное без изменений. Принципиально обработка сообщения
ведётся последовательно, от младших битов к старшим. Однако есть возможность
ускорить обработку сообщения можно, если заметить, что в ряде случаев значение
обрабатываемого триплета позволяет сказать, что несколько следующих триплетов
наверняка не станут особыми. Например, если текущий триплет Тi
= 000, то очевидно, что Тi+1,
Тi+2
не будут особыми, поэтому можно
скопировать все биты данного триплета в результат и переходить к обработке
триплета Тi+3.
Таким образом,
кодирование сообщения может проходить не побитно, а сериями битов. Обозначим за
I вектор, каждый элемент которого Ik равен
числу битов, которые возможно напрямую скопировать при обработке триплета со
значением к. Так, было выяснено, что Iо=3.
Если проанализировать восемь возможных значений триплета, то получится
Iо
= (3,3,1,1,2,2,2,2).
Алгоритм,
осуществляющий обработку сообщения, представлен в таблице 1 на стр. 40. Ниже
будут рассмотрены его свойства, а также будет приведено обоснование начальных
значений переменных р и ![]() .
.
Стоит заметить, что данный алгоритм требует, чтобы ![]() ,
,
однако случай ![]() не
не
представляет интереса (в этом случае закодированное сообщение тождественно
равно исходному сообщению), поэтому его не стоит рассматривать. Также
полагается, что длина сообщения больше двух битов, в противном случае
кодирование является бессмысленным.
Степень точности
задания ![]() определяется
определяется
в алгоритме параметром ![]() ;
;
тем самым, алгоритм гарантирует выполнение условия ![]() <
<
![]() для
для
длинных блоков данных; для коротких блоков статистика может оказаться
неравномерной в силу непредставительности выборки, поэтому данное соотношение
может нарушиться.
Оценим
производительность приведённого алгоритма. Как можно видеть, максимальное
количество арифметических операций, необходимых для обработки одного триплета,
равно 17. А именно, в худшем случае это 3 сравнения, 6 присваиваний, 7 сложений
и одна операция взятия остатка от деления. Из данных операций самая сложная —
это взятие остатка от деления (s mod р), однако если подобрать
такое р, что р = 2а, а € N, то
такая операция превращается в логическую операцию «И» (and), которая по
сложности равна присваиванию.
Полагая за С
максимальное время одной операции, мы получим, что в самом худшем случае
обработка одного бита не займёт более t = 17C времени. Общее
время обработки сообщения длиной N будет удовлетворять условию
Т < 17N. Если С = O(N) (а это, строго говоря,
не справедливо для операции сложения, если иметь в виду её аппаратную
реализацию), то получаем, что скорость работы алгоритма линейная, Т = O(N).
Можно оценить
также среднее число операций, приходящихся на обработку одного бита, для этого
достаточно найти число операций для одного цикла по каждому из восьми
триплетов, а затем найти математическое ожидание с учётом того, что каждый
триплет появляется в сообщении с вероятностью 1/8. Среднее число операций на
алгоритмическом уровне зависит от значений q и р, которые связаны
со значением ![]() по
по
формуле 3 (стр. 45). В результате расчётов на один бит в среднем приходится D(![]() )
)
= ![]() операций.
операций.
Здесь ![]() —
—
число операций в одном цикле алгоритма для триплета к, a ![]() =
=
1/8, так как обрабатывается исходное сообщение, полагаемое распределённым
равномерно. Зависимость D(![]() )
)
нелинейна, она показана на рис. 5. Для наглядного анализа перейдём обратно от ε
к q/p и найдём, что D(q/p) = 10.625 + 0.775q/p,
где 0 ≤ q/p ≤ 1. Таким образом, для всякого
значения ε 10 < D(![]() )
)
< 12, то есть исполнение занимает не более 12 операций. Заметим, что данная
оценка является ориентировочной, поскольку при её получении не учитывается факт
ускорения обработки сообщения с помощью вектора I
в алгоритме.
Алгоритм
декодирования строится таким же образом, которым был построен алгоритм
кодирования, он приведён в таблице 2. Оценивая его производительность, заметим,
что в худшем случае каждый триплет сообщения обрабатывается за 18 операций,
среди которых 3 сравнения, 5 присваиваний, 9 сложений и одно деление с
остатком. Как можно видеть, алгоритм декодирования работает медленнее в худшем
своём случае, чем алгоритм кодирования, однако такой простой расчёт не
учитывает того, что худший случай настает не так уж часто.
Сравнение двух
обратных по сути алгоритмов целесообразно провести по среднему числу операций,
выполняемых для обработки одного бита. Для оценки среднего числа операций для
декодера необходимо принять во внимание тот факт, что в отличие от алгоритма
кодирования, обрабатывающего N бит, алгоритм декодирования для получения
исходного N-битного сообщения должен
обработать N(1 + R(![]() ))
))
бит, где R(![]() )
)
— избыточность кода. Таким образом, среднее количество операций для
декодирования будет равно D(![]() )
)
= ![]()

Таблица
1 – Алгоритм кодирования для потокового кода

Таблица
2 – Алгоритм декодирования для потокового кода
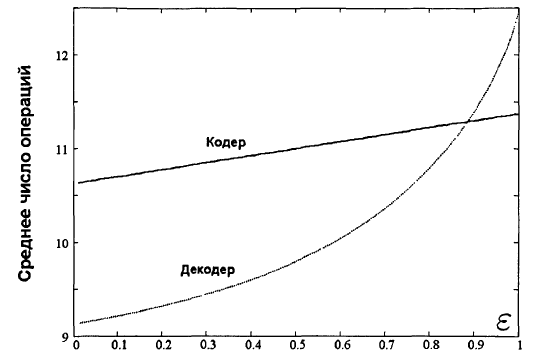
Рисунок
1 – Среднее число операций для потоковых алгоритмов кодирования / декодирования
Библиографический список
1. ГОСТ 2.119-2013. Единая система
конструкторской документации (ЕСКД). Эскизный проект.
2. А.Шафаренко, С.К. Турицын, К.С.
Турицын. Преодоление паттерн-эффекта в оптоволоконных линиях связи с помощью
адаптивного блочного кодирования // Труды ECOC’05, Глазго, 2005, Vol. 2, стр.
193–194
3. Шафаренко А., Турицын К.С., Турицын
С.К. Информационно-теоретический анализ асимметричного кодирования для
подавления
паттерн – эффекта в цифровых технологиях. Связь // IEEE Transactions on Communications,
Vol.
55 (2), 2007.-С. 237-241..

