Предметная подготовка будущего учителя математики предполагает изучение разнообразных разделов высшей математики, на первый взгляд, далеко стоящих от школьного курса. Эта удалённость и высокая абстракция изучаемых понятий часто приводит к снижению мотивации учебной деятельности студентов и непринятию сложных разделов высшей математики как значимых для будущей профессиональной деятельности.
Мотивация основывается на мотивах, под которыми имеются ввиду конкретные побуждения, заставляющие личность действовать. Как отмечается в педагогической литературе, мотивы, стимулирующие студента к учению, могут быть самыми различными. Известно, что одним из познавательных мотивов является создание проблемных ситуаций, решение которых приводит к открытию новых для студента знаний. С этой точки зрения, особый интерес при обучении высшей алгебре будущих учителей математики представляют математические задачи, имеющие «красивые» решения вне элементарной математики. В этой статье речь пойдет о возможностях, предоставляемых высшей алгеброй, и будет подробно разобраны решения двух задач.
Первая задача связана с хорошо известным «египетским треугольником» и звучит так: можно ли его острые углы выразить в целых кратных числа 
?
Обсудим условие задачи. Итак, есть треугольник со сторонами 3, 4 и 5. Так как сумма острых углов равна 
(выражена рациональным кратным ), то достаточно решить вопрос об одном из острых углов. Выберем, например, больший угол – это 
, и обозначим его 
. Требуется, проверить возможность представления 
, где в силу положительного можно считать m и n натуральными числами. Покажем, как с помощью свойств порядка элемента группы установить иррациональность числа 
.
Напомним, что порядком элемента а мультипликативной группы называется наименьшее натуральное число m такое, что 
. Если же 
для любого натурального числа m, то а называется элементом бесконечного порядка [1], [2].
Предварительно докажем, что число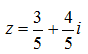 
является элементом бесконечного порядка в мультипликативной группе поля комплексных чисел. Допустим противное, т. е. существует такое натуральное число n, что 
, получим 
. Опираясь на свойства степеней в мультипликативных группах, имеем 
. Преобразуем левую и правую части равенства. Заменим основания степеней 
и, возведём в натуральную степень n, получим: 
. Первоначальное равенство 
примет вид 
. Заметим, что 
(иначе, в силу отсутствия делителей нуля в поле, получим 
, что неверно), сократим равенство на 
, получим 
.
Представим число 4 в виде суммы 
и возведём в степень n 
. Далее используем бином Ньютона для преобразования правой части:
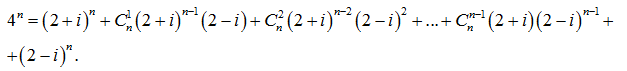
Заменим последнее слагаемое на 
, тогда каждое слагаемое в правой части полученного равенства содержит множитель 
. Значит, правая часть может быть представлена в виде произведения этого числа на некоторое комплексное 
, причем в силу целых коэффициентов рассматриваемого равенства числа a и b также будут целыми. Итак, 
. Перейдем в последнем равенстве к модулям: 
, и вычислив модуль, получим равенство 
. Возведём обе части равенства в квадрат 
. Очевидно, что 
, а это значит, что 
делится на 5, откуда в силу простоты числа 5, получаем, что 4 делится на 5. Противоречие. Значит, предположение о конечности порядка числа 
неверно, т. е. оно является элементом бесконечного порядка в мультипликативной группе комплексных чисел.
Теперь вернёмся к поставленной задаче. Допустим, что число 
является рациональным, т. е.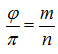 
, где m и n натуральные числа. Перепишем равенство 
. Рассмотрим комплексное число 
. Вычисляя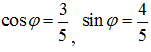 
, получаем 
. Далее по формуле Муавра 
. Сделаем подстановку 
, получим 
Так как 
, то 
и 
, т. е.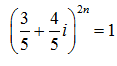 
и число 
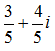имеет конечный порядок в мультипликативной группе поля комплексных чисел, что противоречит доказанному ранее. Предположение, что число 
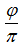является рациональным неверно и доказано, что число 
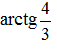не является рациональным кратным .
Вторая задача – олимпиадная задача для школьников, решение которой ученик осуществляет подбором. Такой способ, как правило, требует много времени, и сложно устанавливается единственность решения или доказательство того факта, что подобраны все решения. Итак, задача: можно ли расставить все двенадцать чисел 1, 2,…, 12 по окружности так, чтобы для любых трёх чисел 
стоящих подряд, число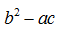 
делилось на 13? Если да, найти все возможные варианты.
Для решения задачи будем использовать общую алгебру и теорию арифметических сравнений. Заметим, что числа, о которых идёт речь в задаче, образуют группу обратимых элементов поля вычетов по модулю 13: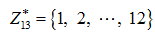 
. Пусть 
тогда по свойству сравнений: 
и условие 
равносильно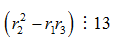 
. Это значит, что числа 
и 
в группе обратимых элементов поля вычетов по модулю 13 совпадают и элементы группы 
образуют геометрическую прогрессию. Покажем, что группа 
– циклическая. Найдём порядок числа 2 в этой группе. По свойству, порядок элемента группы является делителем порядка группы – числа 12. Проверим делители 1, 2, 3, 4, 6, 12:
Порядок числа 2 равен 12. Значит, имеем дело с циклической группой, в которой образующим будет, к примеру, число 2. Представим каждое число степенью с основанием 2 по модулю 13:
Получаем первое решение (рисунок 1):
Чтобы указать оставшиеся решения найдём все образующие в группе 
. В силу свойства порядка элемента группы, элемент, являющийся степенью с показателем n образующего элемента, будет образующим тогда и только тогда, когда окажутся взаимно просты показатель степени n и порядок группы [2]. В нашей задаче, показатель степени должен быть взаимно прост с числом 12, т. е. он может быть равен только 1, 5, 7, 11. Находим ещё три образующих: 
. И три решения (рисунки 2, 3, 4):
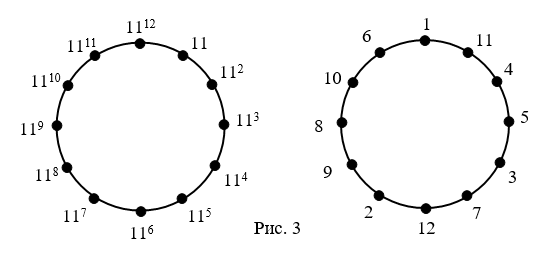
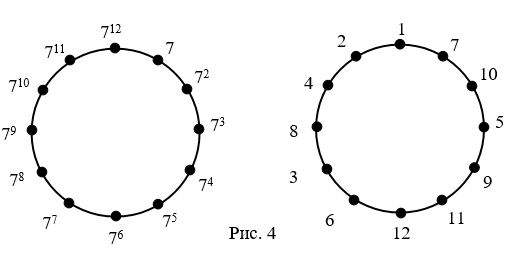
Можно заметить, что решения, приведённые на рисунках 1 и 4 (также 2 и 3) отличаются только порядком записи – по часовой стрелке и против часовой стрелки. Действительно, в 
, решения порождены парами взаимно обратных элементов.
Конечно, можно привести и другие примеры задач элементарной математики, допускающие интересные решения в рамках теорий высшей алгебры, теории чисел, математического анализа. Специально организованная работа над их решениями будет служить формированию у студентов – будущих учителей математики внутренней мотивации к учению. Именно она важна не только для успешного обучения в вузе, но и для дальнейшего профессионального самообразования.
Литература
- Кострикин А. И. Введение в алгебру. Часть I. Основы алгебры: Учебник для вузов. — 3-е изд. — М. : ФИЗМАТЛИТ, 2004. — 272 с.
- Сборник задач по алгебре: Учеб. пособие / Под ред. А. И. Кострикина. — М.: Наука. Гл. ред. физ.-мат. Лит., 1987. — 352 с.
