Ақырлы элемент әдісі – инженерлік және физикалық есептерді шешудің тиімді сандық әдісі. Оның көмегімен сұйықтықтың құбырлардың арқылы, бөгеттері арқылы, кеуекті ортадағы қозғалысы қарастырылады, сығылатын газдың шығуы зерттеледі, электростатика және майлау мәселелері шешіліп, жүйелердің тербелісі талданады. Бұл әдістің пайда болуы ғарыштық зерттеу мәселелерін шешумен байланысты. Ол алғаш рет Тернер, Клуж, Мартин, Топп шығармаларында жарияланды. Әдістің теориялық дамуына 1963 жылы маңызды үлес қосылды. Құрылымдық механикада потенциалдық энергияны азайту арқылы ақырлы элемент әдісі есепті сызықтық тепе-теңдік теңдеуіне дейін азайтуға мүмкіндік береді.
Құрылымдық механика есептерін шешудің сандық процедурасынан алынған ақырлы элемент әдісі дифференциалдық теңдеулерді сандық шешудің жалпы әдісіне немесе дифференциалдық теңдеулер жүйесіне айналды.
Жалпы жағдайда, үздіксіз шама алдын-ала белгілі емес, сондықтан аймақтың кейбір ішкі нүктелерінде осы шаманың мәнін анықтау қажет. Үздіксіз шаманың дискретті моделін құру кезінде келесі әрекеттерді орындаңыз.
Екі өлшемді немесе үш өлшемді доменде анықталған үздіксіз шаманың дискретті моделін құру кезінде ақырлы элемент әдісінің негізгі ұғымы осылай қолданылады. Екі өлшемді жағдайда элементтер (x, y) функциялары арқылы сипатталады, сонымен қатар үшбұрыш немесе төртбұрыш түрінде элементтер жиі қарастырылады. Енді элементтердің функциялары тегіс немесе қисық беттермен бейнеленген. Егер үшбұрышты элемент үшін үш және төрттен тұратын түйін нүктелерінің минималды саны алынса, элементтің функциясы жазықтықпен ұсынылады.
Аймақты қосалқы домендерге бөлу мәселені шешудің алғашқы қадамы болып табылады және бұл қадамның теориялық негіздемесі жоқ. Дененің дискретизациясы нақты дененің дискретті моделін құру үшін қолданылатын қосалқы домендердің санын, мөлшерін және нысанын көрсетуді қамтиды.
Проблемаларды ақырлы элемент әдісімен шешу кезінде әртүрлі типтегі элементтер қолданылады. Қарапайым элемент – бір өлшемді элемент. Схема кесінді түрінде болса да (1, а) кесінді түрінде бейнеленген. Көлденең қиманың ұзындығы әртүрлі болуы мүмкін, бірақ көптеген тапсырмаларда ол тұрақты болып саналады. Қарапайым бір өлшемді элементте екі түйін бар, олардың әрқайсысында біреуі болады. Жоғары (b, c) суретте үш түйінді және төрт түйіннің элементтері бейнеленген. Бір өлшемді элементті иілуге болады, егер парфюмерия ұзындығы элементтерді анықтайтын теңдеулерге енсе.
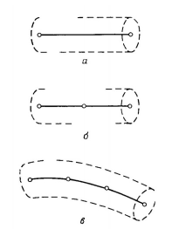
1-сурет. Бір өлшемді ақырлы элементтер
Екі өлшемді аймақтың дискретті моделін құру үшін элементтердің екі негізгі тобы қолданылады: үшбұрыш және төртбұрыш. Әр отбасының сызықты элементтерінің жақтары түзу сызықтар (2, а). Квадрат және кубтық элементтердің тіктөртбұрышты немесе қисық жағы немесе екеуі де болуы мүмкін (2, b). Иілген жиектерді модельдеу мүмкіндігіне элементтердің бүйірлерінің ортасына түйіндер қосу арқылы қол жеткізіледі. Элементтердің екі жанұясын бір уақытта аймақтың ішінде қолдануға болады, егер олардың бүйірлерінде түйіндер бірдей болса (2, c). Элементтің қалыңдығы тұрақты болуы мүмкін немесе координаттар функциясы болуы мүмкін.
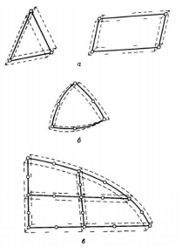
2-сурет. Екі өлшемді ақырлы элементтер
Ең көп таралған үш өлшемді элементтер – бұл тетраэдр және параллелепипед (3, a, b). Екі жағдайда да сызықтық элементтер шекара ретінде қисық беттерге ие болуы мүмкін. Үшөлшемді денені бөлу кезінде элементтердің орналасуы мен дискретті модельді елестету қиын, сондықтан параллелепипед, бәлкім, элементтердің осы екі түрінің ең қажеті болып табылады.
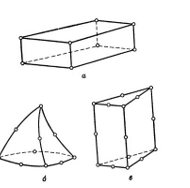
3-сурет. Үш өлшемді ақырлы элементтер
Cуретте көріп тұрғанымыздай цилиндр пішінді (3, c) денелерді қарастыру кезінде қолданылатын элементтердің тағы бір көрінісі көрсетілген. Бұл элементтер екі өлшемді үшбұрышқа ұқсас және үшінші координат бойында белгісіз шаманың өзгеруін ескеруге мүмкіндік береді. Аксиметриялық есептерде (4) кең қолданылатын элемент көрсетілген. Бұл элемент үшбұрышты бұру арқылы қолданылады. Ұқсас элементті төртбұрышты айналдыру арқылы алуға болады.
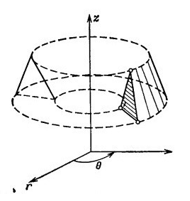
4-сурет. Аксиметрлік ақырлы элемент
Пайдаланылған әдебиеттер тізімі
- Ларри Дж. Сегерлинд. Прикладной конечно-элементный анализ. – Джон Уилли и Сыновья, Inc. Нью-Йорк / Лондон / Сидней / Торонто, 1976.- 392 с.
- Carslaw H.S., Jaeger J.C. Теплопроводность в твердых телах. Издательство Оксфордского университета, Лондон, 1986 – 526 с.
- Тимошенко С., Гудиер Дж. Н. Теория упругости. МакГроу-Хилл. Книга. Компания. Inc., 1987. – 567 с.
- Зенкевич О.С. Метод в инженерных науках. Butterworth-Heinemann. – Оксфорд-Окленд-Бостон-Йоханнесбург-Мельбурн-Нью-Дели, 2000. – 690 с

