МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ПО ОПРЕДЕЛЕНИЮ ПРОЧНОСТИ ЛЬДА МЕТОДОМ ЦЕНТРАЛЬНОГО ИЗГИБА

Цель: определение прочности льда на центральный изгиб на полевой испытательной машине ПИМ-200М (рисунок 1). Обработка данных эксперимента.

Порядок выполнения работы

1.   Познакомиться с требуемым оборудованием.

2.   Ознакомиться с методикой проведения эксперимента.

3.   Провести корреляционный анализ экспериментальных данных.

4.   Определить зависимость, описывающую экспериментальные данные, полученные в результате наблюдения (для выбора исходных данных использовать таблицу П1 и П2).

МЕСТО ПРОВЕДЕНИЯ

Г. Владивосток, Приморский край, бухта Мелководная.

НЕОБХОДИМОЕ ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ

·          полевая испытательная машина ПИМ-200М (рис. 1);

·          керноотборник «KovacsEnterprise»;

·          станок для распиловки кернов на диски заданной толщины;

·          линейка;

·          штангенциркуль;

·          термометр.

Назначение ПИМ-200М: Служит для определения прочности льда на центральный изгиб.

Основные технические характеристики ПИМ-200М

Рисунок 1 — Полевая испытательная машина ПИМ-200М.

ОБЪЕКТ ИССЛЕДОВАНИЯ

Лед в бухте мелководная (рис. 2)

Рисунок 2 – Внешний вид льда

2. МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

Образцы льда в виде круглых пластин изготавливаются из кернов диаметром 141 мм, полученных с помощью керноотборника «KovacsEnterprise». Керн распиливался на специальном станке без пропусков на пластины толщиной 1,5-2,0 см (рисунок 3).

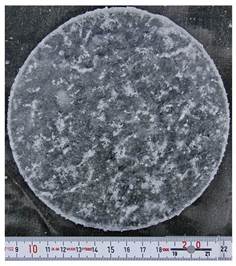
Рисунок 3 – Пластины из кернов

В случае ограниченного времени испытываются образцы, вырезанные из верхней, средней и нижней частей керна по пять пластин с каждого уровня. В некоторых случаях пластины могут вырезаться в соответствии с характерными текстурными особенностями керна. Применялся тот же станок, что и для приготовления цилиндрических образцов льда для испытаний прочности при сжатии. В начале и конце измерений тарировка пресса производится с помощью образцового динамометра. Испытания проводятся при постоянной скорости деформирования. Продолжительность нагружения составляет единицы секунд. Это обеспечивает хрупкое разрушение пластин льда. Максимальное значение силы в момент разрушения образца измеряется по показаниям динамометра со стрелочным индикатором часового типа.

Напряжение в центре круглой свободно опертой пластины постоянной толщины определяется по формуле:

,

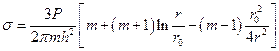где: s – напряжение (кг/см²); Р – нагрузка (кг); m – величина, обратная коэффициенту Пуассона и равная примерно 3; h – толщина пластины (cм); r – радиус пластины (см); r₀ – радиус распределения нагрузки (см).

При испытаниях пластин, приготовленных из ледяного керна диаметром 14,1 см, применяется подставка с внутренним диаметром 12,4 см (r = 6,2 см), а диаметр нагрузочного цилиндра составляет 1 см (r₀ = 0,5 см).  При этом используется простая формула:

где s_пл – разрушающее напряжение (кг/см²), Р_макс – разрушающая нагрузка (кг).

Для льда при температуре воздуха близкой к 0 °С пластины испытываются по мере их изготовления.

Измерения пределов прочности круглых пластин (дисков) льда при испытаниях на центральный изгиб с постоянной скоростью деформирования проводятся в точках отбора образцов для изучения физических свойств льда. Полученные при испытаниях результаты заносятся в таблицу, см таблица 1 Журнал испытаний, по данным которых строятся графики распределения предела прочности круглых пластин по толщине льда.

Замеры следует произвести не менее чем с 3х разных кернов.

Полигон Владивосток

Испытания льда на центральный изгиб

Дата испытания ______

Толщина снега ___ см. Температура воздуха _____ град.

Температура снега на поверхности ____град. Температура льда на границе со снегом ____ град.

Толщина льда _____см. Превышение льда над уровнем воды _____см.

Скорость испытаний на центральный изгиб 2.5 мм/сек, 0.5мм/сек

Таблица 2

3. корреляционный анализ экспериментальных данных

Корреляционный анализ – статистический метод оценки формы, знака и тесноты связи исследуемых признаков или факторов. Совместную изменчивость разных признаков называют «корреляция».

В задачу статистического анализа входят выявление величины корреляционной связи и установление ее типа.

Один из основных коэффициентов, измеряющих связь между варьирующими признаками х и у, является коэффициент корреляции r, который находятся в пределах от 0 до ± 1.

Коэффициент корреляции определяется по следующему выражению:

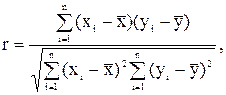                                    (1)

где  – значение единичного результата и средняя арифметическая одного признака;  – значение единичного результата и средняя арифметическая другого зависимого признака.

По значению коэффициента корреляции определяют характер корреляционной связи (табл. 2).

Таблица 2

Сила и характер связи между параметрами

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза H0 о равенстве коэффициента корреляции нулю (rxy = 0). При проверке этой гипотезы используется t-статистика.

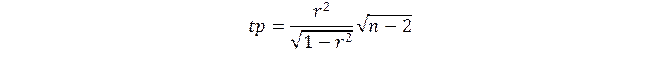
Если расчетное значение tp больше табличного значения tα, то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а, следовательно, о статистической существенности зависимости между х и у. Рассматриваемый критерий используется при числе наблюдений n < 50 При числе наблюдений n > 100 можно применить другую форму t-статистики.

4. Пример выполнения корреляционного анализа (в excel)

1. Собираем данные, полученные в ходе экспериментов, и заносим в таблицу. По горизонтали мы записываем количество образцов полученных после резки керна, по вертикали скорости воздействия на пластинку (рис 4,5).

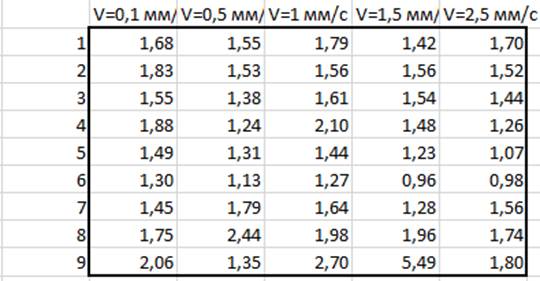
Рисунок 4 — Прочность

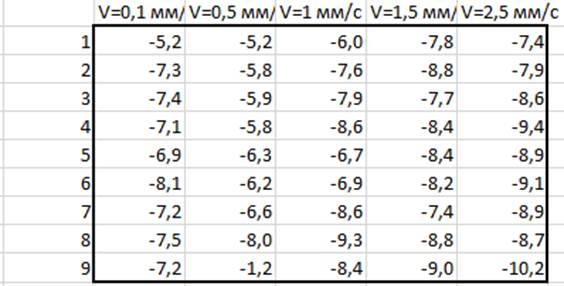
Рисунок 5 — Температура

2. При помощи функций Excel проводим корреляцию температуры и прочности по скорости нагружения (рис 6).

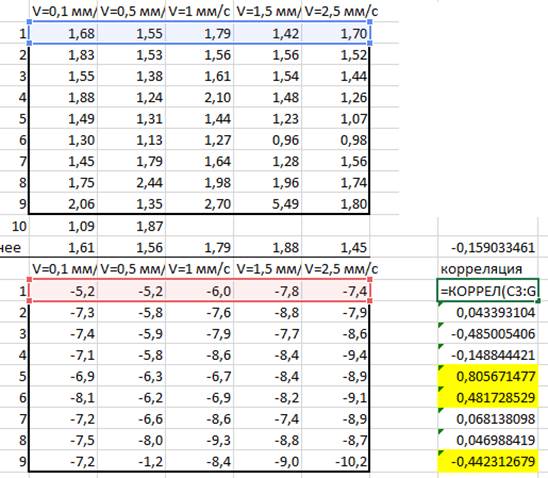
Рисунок 6 — Корреляция температуры и прочности по скорости нагружения

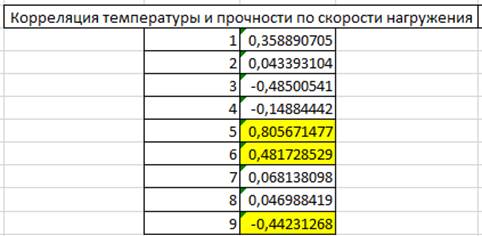
3. Проводим корреляцию температуры и прочности послойно (рис 7).

Рисунок 7 — Корреляция температуры и прочности послойно

Контрольные вопросы

1.Какое требуется оборудование для проведения экспериментов по определению прочности льда на центральный изгиб?

2.Методика проведения эксперимента по определению прочности льда на центральный изгиб?

3. Что такое корреляционный анализ?

4. Что означает знак и величина коэффициента корреляции?

лИТЕРАТУРА

1. Боровиков В.П., Боровиков И.П. STATISTICA – Статистический анализ и обработка данных в среде Windows. – М.: Информационно-издательский дом «Филинъ», 1998.

2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для студентов вузов. — М.: Высш.шк.. — 2000. — 479с.

3. Львовский Е.Н. Статистические методы построения эмпирических формул: Учебное пособие для вузов. — М.: Высш. школа,1988 -239 с.

4. Практическое использование Microsoft Excel для обобщения статистических данных.