Важным моментом транспортного процесса предприятия является планирование перевозок. Это объясняется как сокращением длительности циклов коммерческих операций, так и увеличением стоимости хранения, необходимостью реагирования на изменение потребительского спроса. Для решения этого вопроса необходима оптимизация проектирования доставки и планирование перевозок, чтобы привлечь клиентов [1].
Для снижения транспортных затрат, доставки грузов в срок, максимального удовлетворения всех требований заказчика перевозок необходима конкретизация и детализация организационных мероприятий, связанных с перевозкой (выбор маршрута и вида транспорта в зависимости от типа груза) [2].
Предложенный метод оптимизации грузоперевозок применим к транспортным логистическим компаниям, обладающим определенным парком транспортных средств.
Пусть заданы следующие условия:
1. Компания обладает парком из n транспортных средств, каждое из которых обладает следующими характеристиками:
·Грузоподъемность, т;
·Вместимость, 
.
2. Есть m заявок (заказов) на перевозку грузов, из которых нужно выбрать наиболее выгодные к перевозке. Каждый груз обладает следующими характеристиками:
·Вес, т;
·Удельный объем, 
;
·Удельная прибыль с перевозки, $/т.
Предполагается, что заявку можно либо принять, либо отклонить, т.е. нельзя перевезти только часть груза; грузы также нельзя делить на части [3].
Необходимо составить оптимальный план грузоперевозки и определить наиболее прибыльные грузы. Для решения задачи, воспользуемся методом линейного программирования.
Постановка задачи выглядит следующим образом:
Целевая функция максимизирует суммарную прибыль от перевозок.
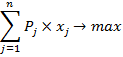
Где 
– удельная прибыль ($/тонну);
— объем перевозки (тонн);
В задаче имеются 3 группы ограничений:
1. Ограничения по весу груза в транспортном средстве
– ограничение по грузоподъемности i-го транспортного средства, т.
2. Ограничения по объему груза в транспортном средстве
– удельный объем j-го груза, 
;
– ограничение по вместимостиi-готранспортного средства, 
.
3. Ограничения по общему объему груза
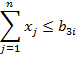
– ограничение по общему объему груза, т.
Проиллюстрируем предложенную задачу примером.
Пусть у транспортной компании имеется 3 транспортных средства, характеристики которых представлены в таблице 1.
Таблица 1. Исходные данные по транспортным средствам.
| Транспортное средство | Предел по весу(тонн) | Предел по объему() |
| 1 | 30 | 700 |
| 2 | 22 | 1000 |
| 3 | 16 | 400 |
Имеется шесть заявок на перевозку грузов. Веса, объемы грузов и ожидаемая прибыль даны в таблице 2.
Таблица 2. Исходные данные по грузам.
| Груз | Вес(тонн) | Удельный объем(/тонну) |
Прибыль($/тонну) |
| 1 | 10 | 15 | 200 |
| 2 | 13 | 40 | 400 |
| 3 | 11 | 30 | 360 |
| 4 | 18 | 35 | 290 |
| 5 | 9 | 45 | 340 |
| 6 | 8 | 20 | 250 |
Необходимо:
· Выбрать к перевозке наиболее выгодные грузы
· Распределить грузы по транспортным средствам
При этом, нужно максимизировав суммарную прибыль от перевозок. В таблице 3 представлена целевая функция в табличном виде и найденные по результату решения коэффициенты.
Таблица 3. Целевая функция прямой задачи
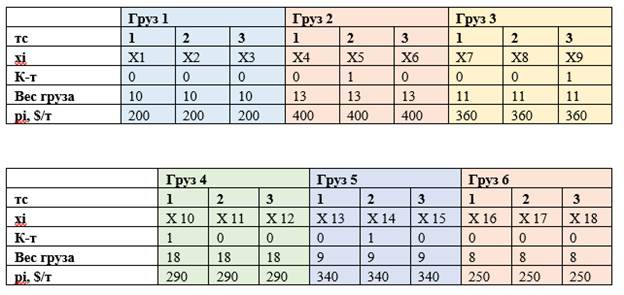
Для решения задачи был использован бинарный коэффициент, чтобы удовлетворить условию неделимости грузов на части (значение 1 – груз принят к перевозке, 0 – груз не принят к перевозке). Таким образом, искомые значенияXiцелевой функции представляют собой произведение бинарного коэффициента и заданного в условии веса груза [4].
Решение данной задачи показало, что максимальная прибыль при перевозке составляет 17440денежных единиц. К перевозке приняты грузы 2, 3, 4 и 5. При этом учтены все ограничения (таблица 4).
Таблица 4. Ограничения к задаче
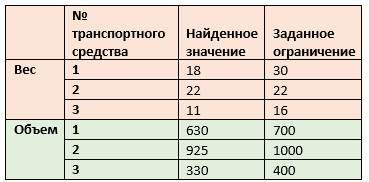
Как видно из таблицы, найденный план перевозок не превышает заданные значения характеристик транспортных средств.
Для определения наиболее выгодных грузов с точки зрения прибыли, а также характеристик имеющегося автопарка, составим двойственную задачу.
Целевая функция и двойственные оценки (Y1-Y12) двойственной задачи представлены в таблице 5.
Таблица 5. Целевая функция и двойственные оценки двойственной задачи
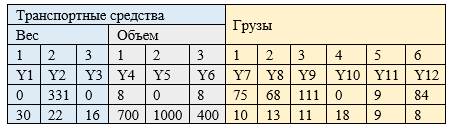
Значение целевой функции составило 20031 денежные единицы. По теореме двойственности, значения целевой функции прямой и обратной задач должны совпадать, но в представленном примере значение функции двойственной несколько выше. Это связано с тем, что в прямой задаче присутствует бинарный коэффициент, учитывающий неделимость груза, который и уменьшает значение прибыли.
Сделаем выводы по полученным двойственным оценкам. Поскольку статья посвящена выбору оптимального плана перевозок, рассмотрим оценки по грузам (Y7-Y12). Чем больше значение оценки у груза, тем выгоднее он для перевозки с точки зрения получения максимальной прибыли. На первый взгляд, наиболее прибыльным является груз 2, потому что он обладает наибольшей удельной прибылью. Тем не менее, наибольшее значение двойственной оценки мы видим у груза 3, следовательно, он и является приоритетным при составлении плана перевозки. Данное противоречие обусловлено тем, что у груза 3 меньше удельный объем, соответственно и полезного объема в транспортном средстве он занимает меньше. Стоит заметить, что полученное значение справедливо только для конкретного парка транспортных средств [5]. Так, при увеличении объема грузового отсека при сохранении грузоподъемности, груз 2, обладающий наибольшей прибыльностью с единицы массы, может стать наиболее выгодным.
Таким образом, по результатам решения прямой задачи линейного программирования был составлен оптимальный план перевозок грузов. Решение двойственной задачи показало наиболее выгодные грузы с точки зрения имеющихся транспортных средств у компании. Анализ полученных оценок показал, что не всегда грузы с самыми большими удельными показателями прибыли могут принести максимальный доход компании. Предлагаемая методика позволяет составить план перевозок с учетом не только прибыли, но и технических характеристик транспортных средств, параметров грузов; прочие факторы также могут быть учтены посредством добавления новых ограничений в задачу линейного программирования. Полученные двойственные оценки удобны тем, что они могут быть использованы для определения приоритета выбора грузов при внесении изменений в заказы без повторного решения прямой задачи линейного программирования.
Использованные источники:
1. Организация перевозок грузов. — М.: Academia, 2015. — 304 c.
2. Ашманов, С.А. Линейное программирование / С.А. Ашманов. — М.: 2013. — 767 c
3. Горев, А. Э. Грузовые перевозки. Учебник / А.Э. Горев. — М.: Academia, 2013. — 304 c.
4. Просветов, Г. И. Математические методы в логистике. Задачи и решения / Г.И. Просветов. — М.: Альфа-пресс, 2017. — 304 c
5. Юдин, Д. Б. Задачи и методы линейного программирования. Задачи транспортного типа / Д.Б. Юдин, Е.Г. Гольштейн. — М.: Либроком, 2013. — 184 c.
