1. Введение
Внимание экспертов всегда было сосредоточено на пространственных явлениях, таких как: проблемы со столкновением, оптимизация топлива, гравитационные маневры и т. Д., Эти исследования были успешными благодаря математическому моделированию. Понятно, что эта задача была непростой из-за ряда проблем, связанных со сложностью математического описания относительного движения космических аппаратов, то есть при создании математических моделей, которые могли бы описать относительное движение этих космических аппаратов. В 1960 году Клохесси и Уилтшир создали математическую модель, которая могла бы описать относительное движение космических аппаратов вблизи круговых орбит [1, 2]. Эти уравнения были позднее модифицированы Хиллом, поэтому сегодня они называются HCW (Хилл-Клохесси-Уилтшир) [4, 18, 19].
В работе Хилла и других ученых отсутствует подход к компонентам возмущающих сил, то есть они не анализировали случай, когда один из компонентов этих возмущающих сил равен нулю, поэтому в данной статье автор рассмотрит этот частный случай, когда составляющая возмущающих сил x равна нулю.
2. Постановка задача
Для анализа движения двух космических аппаратов по орбитам, близким к Земле, автор ввел орбитальную систему координат. Рассмотрим два космических аппарата (Ангосат-3 и Angospace), но Angospace (целевой космический аппарат), движущийся по орбите радиуса 
, повторяющих вокруг Земли. Космический аппарат — Ангосат-3 (маневрирующий космический аппарат), движущийся по другой орбите с радиусом 
.
Необходимо найти аналитическое решение математической модели, которая описывает движение этих двух космических аппаратов по орбитам, близким к Земле, чтобы приблизиться к их положениям и скоростям.
3. Математическая модель
В качестве математической модели рассмотрим систему дифференциальных уравнений второго порядка (модель Клохесси-Уилтшира-Хилла). Тем не менее, давайте рассмотрим, что уравнения Клохесси-Уилтшира-Хилла линеаризуются, и что мы проанализируем частный случай, то есть когда составляющая возмущающей силы на оси 
равна нулю (
).
Для решения задачи, представленной на рисунке 1, автор представляет систему координат Хилла, связанную с Angospace (целевой космический аппарат) и Ангосат-3. Ось x направлена вдоль вектора радиуса Angospace в одной тоже направление, ось y направлена вдоль вектора скорости Angospace (целевой космический аппарат), а ось z перпендикулярна целевого космического аппарата.
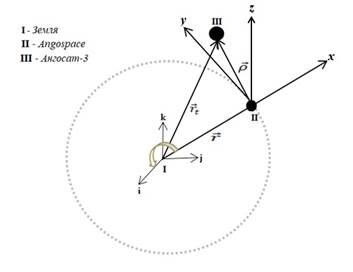
Рис. 1. Система координат Хилла.
Поскольку целевой космический аппарат (Angospace) находится на круговой орбите, 
и являются постоянными, таким образом, согласно Bate et. и др. (1971).
(1)
Где: — угловая скорость (среднее движение), 
— стандартный гравитационный параметр Земли, 
, — расстояние от центра масс Земли до Ангосата-3, — расстояние от центра масс Земли до Angospace и 
— относительное расстояние между Ангосат-3 и Angospace.
Таким образом, можно записать уравнения Хилла-Клохесси-Уилтшира следующим образом:
(2)
(3)
(5)
В этой статьи рассматривается случае, когда , то есть:
(6)
(7)
(8)
4. Метод преобразования Лапласа
Обычное дифференциальное уравнение — это уравнение, которое включает функцию переменной и ее производных:
(9)
Если дифференциальные уравнения дополняются начальными условиями, то они называются задачей начальных значений.
Преобразование Лапласа предоставляет методологию для решения и анализа задач, включающих обыкновенные дифференциальные уравнения, а также системы обыкновенных дифференциальных уравнений.
(10)
Метод преобразования Лапласа состоит в использовании преобразования Лапласа для преобразования дифференциального уравнения в простую задачу через свойства преобразования Лапласа. Как правило, в линейных уравнениях постоянных коэффициентов (дифференциальные уравнения модели HCW) преобразуются в алгебраические уравнения, в которых нужно просто изолировать полученное неизвестное, и с помощью повторения обратных преобразований Лапласа мы найдем исходное решение.
4.1. Свойства преобразования Лапласа производной
Аналогично, если 
– они непрерывны и 
непрерывен по частям тогда:
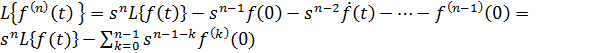(11)
Поскольку дифференциальные уравнения модели HCW являются обычными и имеют вторую степень, то из уравнения (11) получаются следующие выражения:
(11a)
(11b)
5. Решение уравнений HCW
Однако рассматриваемая модель может быть представлена в пространстве состояний как:
Уравнение (12) можно записать в виде матрицы:
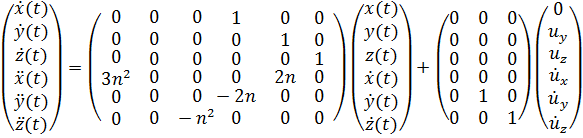(13)
; 
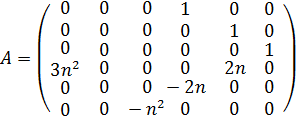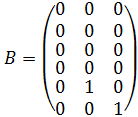
где: 
— вектор состояния; 
, 
— вектор реактивного ускорения. В этой статье мы рассмотрим, что 
Модель HCW представляет собой систему из трех обыкновенных дифференциальных уравнений второго порядка для решения уравнений HCW, важно отметить, что уравнения (6) и (7) связаны друг с другом, поэтому будет удобно разделять движения: вне орбитальной плоскости H-Миру (компонент z) и в орбитальной плоскости RV-Миру (компонент xy), Таким образом, для решения система делится на две подсистемы: одну Каландула (H-Миру) и другую Камбонду (RV— Миру).
5.1. Модель Камбонду для передвижения в RV— Миру
Здесь подсистема представлена четырьмя состояниями, содержащими два входа и два выхода. Это плоское движение, связанная динамика из уравнения. (12) выглядит следующим образом, с вектором состояния 
:
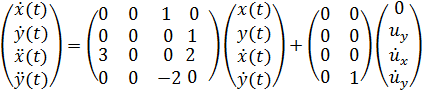(14)
; 
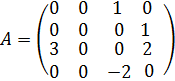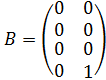
где: 
обозначают положение и 
скорость соответственно.
Таким образом, используя метод преобразования Лапласа для модели Камбонду, мы имеем:
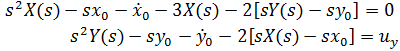(15)
Автор сформирует систему из двух уравнений, для ее решения будет использовать метод подстановки (изолировать Y(s) во втором уравнении и подставить в первое уравнение той же системы), будет иметь вид:
(16)
(17)
Чтобы найти общее решение этой модели, будет использовать обратное преобразование Лапласа, например:
(18)
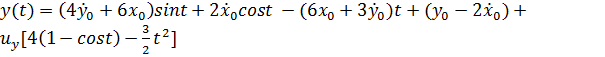(19)
5.2. Модель Каландула для передвижения в H-Миру
Здесь подсистема представлена двумя состояниями, содержащими вход и выход. Внеплановая динамика из уравнения (12) выглядит следующим образом, с вектором состояния 
(20)
; 
где: 
— обозначает положение и 
скорость соответственно.
Таким образом, используя метод преобразования Лапласа для модели Каландула, имеет:
(21)
Уравнение (21) является линейным уравнением в 
, то есть
(22)
Чтобы найти общее решение для этой модели, будет использовать обратное преобразование Лапласа, например:
(23)
6. Производные уравнений HCW
Производная — это мгновенная скорость изменения функции, то есть
, 
и 
(24)
Далее автор представит производные уравнений HCW для обеих моделей.
6.1. Для модели Камбонду
(25) 
(26)
6.2. Для модели Каландула
(27)
Матрица распространения, предварительно умножающая вектор начальных условий, также называется матрицей перехода состояний для уравнений CW. Эта матрица помечена как 
– фундаментальная матрица и изменяется во времени. Тогда можно записаться таким образом:
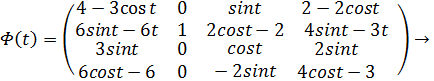Модель Камбонду
Модель Каландула
7. Заключение
В этой статье автор представлял аналитическое решение дифференциальных уравнений Клохесси-Уилтшира-Хилла, для случая, когда составляющая возмущающих сил x равна нулю. В качестве аналитического метода он использовал метод преобразования Лапласа, а также его обратное. Это частный случай, поскольку автор идеализирует, что движение космического аппарата, в котором на него действует возмущающая сила, однако его компонент в x равен нулю, можно идеализировать, что у космического аппарата будет ограниченное движение в зависимости от других компонентов. Это так, поэтому автор рекомендует сделать то же самое с численными методами и графическое представление движения этого космического аппарата. Благодаря этому решению у нас есть открытый путь для продолжения исследования и решения различных проблем, таких как: оптимизация траекторий, проблемы захода на посадку и встречи и т. Д.
8. Список литературы/ References
1. Бейт Р.Р.; Мюллер, Д.Д.; Уайт Дж. Э. (1971). Основы астродинамики. Нью-Йорк, США: Dover.p.455.
2. Клохесси, W. H .; Уилтшир, Р. С. (1960). Терминальная система наведения для спутниковой встречи. Журнал аэрокосмических наук, т. 27, н. 9, стр. 653-659.
3. Фехсе, В. (2003). Автоматическое сближение и стыковка космического корабля. Нью-Йорк, США: издательство Кембриджского университета. П. 517.
4. Джентина, Дж. (2009). Десенволвименто и симуляция похода за Маноброй рандеву и стыковка с платформой Орбитальное восстановление САРА.
5. Клохесси, W. H. и Уилтшир, R.S., «Руководство по терминалу для спутниковой встречи», J. Aerospace Sciences, Vol. 27 (1960), p. 653.
6. Ручинская Е. В. Математическое моделирование управляемого движения космических аппаратов: Дисс. канд. техн. наук: Спец : 05.13.18 / Е. В. Ручинская ; МАТИ . ‒ М .: 2010. – 175 с .
7. Гродзовский Г.Л., Иванов Ю.В. Н. и Токарев, В. В., «Механика космического полета малой тяги», NASA TTF-507, 1969, XIV с.3.
8. Клохесси, W. H. и Уилтшир, R. S., «Система наведения терминала для спутниковой встречи», J. Aerospace Sci., 27 (9), 1960, pp. 653-658. DOI: https://doi.org/10.2514/8.8704.
9. Маринеску, Ал., «Оптимальное орбитальное рандеву с малой тягой», J. Spacecraft, 13 (7), 1976, с.385-392. DOI: https://doi.org/10.2514/3.27913.
10. Картер Т. и Хуми М. Уравнения Клохесси-Уилтшира, модифицированные для включения квадратичного сопротивления, Дж. Гуид. Control Dyn., 25 (6), 2002, pp.1058-1063. DOI: https://doi.org/10.2514/2.5010.
11. Клохесси, W. H. и Уилтшир, R.S., «Руководство по терминалу для спутниковой встречи», J. Aerospace Sciences, Vol. 27 (1960), p. 653.
