Одним из главных понятий, которым мы будем пользоваться, является производящая функция. Введем следующее определение:
Пусть ![]() – произвольная (бесконечная) последовательность чисел. Формальный степенной ряд
– произвольная (бесконечная) последовательность чисел. Формальный степенной ряд ![]() называется производящей функцией этой последовательности.
называется производящей функцией этой последовательности.
Понятие формального степенного ряда выходит за рамки данной учебной работы. Приведем здесь лишь неформальные и интуитивные соображения, касающиеся данного понятия. Так, заметим, что, употребляя слово «функция», мы вовсе не имеем в виду, что написанное выражение действительно является функцией. Переменная ![]() является формальной, и сумма ряда
является формальной, и сумма ряда ![]() смысла не имеет. Однако верно утверждение
смысла не имеет. Однако верно утверждение ![]() , т. е. мы знаем значение производящей функции в нуле. Скорее
, т. е. мы знаем значение производящей функции в нуле. Скорее ![]() является просто иным обозначением последовательности
является просто иным обозначением последовательности ![]() , удобным в отношении некоторых аспектов.
, удобным в отношении некоторых аспектов.
Чтобы пояснить представленное выше определение, рассмотрим следующий пример:
Пусть задана последовательность ![]() . Производящая функция этой последовательности:
. Производящая функция этой последовательности: ![]() . Перед нами бесконечная геометрическая прогрессия, которая равна
. Перед нами бесконечная геометрическая прогрессия, которая равна ![]() . Другими словами,
. Другими словами, ![]() , при этом выражение
, при этом выражение ![]() называется замкнутым видом производящей функции.
называется замкнутым видом производящей функции.
Замечание: в дальнейшем мы будем стараться приводить производящие функции к замкнутому виду.
Укажем теперь, в каких целях мы будем использовать производящие функции:
Производящая функция позволяет нам решать задачу вывода не рекуррентной формулы для элементов последовательности. Иными словами, из рекуррентного уравнения для последовательности мы можем с помощью производящей функции получить формулу, которая по заданному номеру будет возвращать элемент последовательности с этим номером. В работе будут приведены примеры, иллюстрирующие данное утверждение.
Еще одно преимущество производящей функции – с ее помощью операции над последовательностями делаются легче.
В связи с этим, рассмотрим основные операции над производящими функциями.
1. Умножение каждой из производящих функций ![]() и
и ![]() на константу и сложение полученных результатов:
на константу и сложение полученных результатов:
Предположим, что ![]() – производящая функция последовательности
– производящая функция последовательности ![]() , а
, а ![]() – производящая функция последовательности
– производящая функция последовательности ![]() .Следовательно,
.Следовательно, ![]() можно записать в виде:
можно записать в виде: ![]() , а
, а ![]() соответственно будет равно
соответственно будет равно![]() , тогда
, тогда![]() . Таким образом, получаем, что выражение
. Таким образом, получаем, что выражение ![]() – это производящая функция для последовательности
– это производящая функция для последовательности ![]() .
.
2. Сдвиг последовательности вправо на m позиций.
Рассмотрим последовательность ![]() , для нее мы можем записать производящую функцию:
, для нее мы можем записать производящую функцию: ![]() Построим новую производящую функцию для последовательности
Построим новую производящую функцию для последовательности ![]() , начинающейся с m нулей:
, начинающейся с m нулей: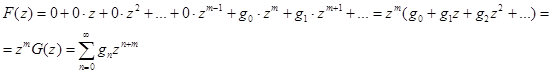
3. Сдвиг последовательности влево на m позиций. Другими словами, мы должны вывести новую производящую функцию для последовательности ![]() , из которой удалены первые m элементов.
, из которой удалены первые m элементов.
Рассмотрим на определенном примере. Пусть исходная последовательность представлена в следующем виде ![]() , для нее производящая функция
, для нее производящая функция ![]()
После удаления первых двух элементов из исходной последовательности, мы получим новую последовательность:![]() . Производящая функция этой последовательности примет вид:
. Производящая функция этой последовательности примет вид:
![]()
В общем случае, то есть при удалении m элементов из последовательности, получим следующее выражение для производящей функции:

4. Умножение z на константу.
![]() , таким образом, мы получили производящую функцию последовательности
, таким образом, мы получили производящую функцию последовательности ![]() . Обратим внимание на частный случай, когда
. Обратим внимание на частный случай, когда ![]() . Отметим, что, если мы нашли производящую функцию
. Отметим, что, если мы нашли производящую функцию ![]() для последовательности
для последовательности ![]() , то находить производящую функцию для последовательности
, то находить производящую функцию для последовательности ![]() не нужно, она равна
не нужно, она равна ![]() .
.
5. Часто оказывается важным добавить к коэффициентам множитель n. Данная операция соответствует почленному дифференцированию.
![]() Поясним выше сказанное на примере: Пусть дана последовательность
Поясним выше сказанное на примере: Пусть дана последовательность ![]() и ее производящая функция
и ее производящая функция ![]() в замкнутом виде:
в замкнутом виде: ![]() . Нужно найти производящую функцию последовательности
. Нужно найти производящую функцию последовательности ![]() , для этого возьмем производную от исходной производящей функции:
, для этого возьмем производную от исходной производящей функции: ![]() – замкнутый вид производящей функции последовательности
– замкнутый вид производящей функции последовательности ![]()
6. Чтобы поделить элементы последовательности на n, воспользуемся обратной операцией – интегрированием.
 .
.
7. Умножение производящих функций.
Пусть дана последовательность ![]() и последовательность
и последовательность ![]() , составим для них производящие функции:
, составим для них производящие функции:![]()
![]()
Умножим:![]()
коэффициент при ![]() будет иметь следующий вид:
будет иметь следующий вид: ![]() , тогда, продолжая равенство, получим:
, тогда, продолжая равенство, получим:
![]()
Полученная сумма есть производящая функция свертки последовательностей ![]() и
и ![]() .
.
Следующим важным понятием являются рекуррентные уравнения. Перейдем к их рассмотрению.
Выражение вида ![]() – называется рекуррентным уравнением порядка k для последовательности
– называется рекуррентным уравнением порядка k для последовательности ![]() . Заметим, однако, что наиболее разработана теория линейных стационарных рекуррентных уравнений, в которых функция
. Заметим, однако, что наиболее разработана теория линейных стационарных рекуррентных уравнений, в которых функция ![]() линейна и не зависит от
линейна и не зависит от ![]() . Однородное линейное стационарное рекуррентное уравнение порядка k имеет следующий вид:
. Однородное линейное стационарное рекуррентное уравнение порядка k имеет следующий вид: ![]() ,
,
где ![]() – некоторые числа. Множество решений линейного стационарного рекуррентного уравнения порядка k, образует k-мерное векторное пространство. Достаточно найти k линейно независимых решений, и у нас получится базис. Таким образом, мы можем выразить любое решение как линейную комбинацию базиса. Базисные решения будем искать в виде
– некоторые числа. Множество решений линейного стационарного рекуррентного уравнения порядка k, образует k-мерное векторное пространство. Достаточно найти k линейно независимых решений, и у нас получится базис. Таким образом, мы можем выразить любое решение как линейную комбинацию базиса. Базисные решения будем искать в виде ![]() . Подставляя такое решение в уравнение
. Подставляя такое решение в уравнение ![]() , получим характеристическое уравнение
, получим характеристическое уравнение
![]() или
или ![]() . Решив это характеристическое уравнение, найдем корни
. Решив это характеристическое уравнение, найдем корни ![]() (считаем, что все корни разные).
(считаем, что все корни разные).
 – k различных решений рекуррентного уравнения. Они линейно независимы.
– k различных решений рекуррентного уравнения. Они линейно независимы.
Тогда общее решение рекуррентного уравнения имеет вид: ![]() . Осталось найти
. Осталось найти ![]() .
.
Покажем, что если заданы k начальных условий (т.е. даны числа ![]() ), то решение такой задачи можно выразить явно следующим путем:
), то решение такой задачи можно выразить явно следующим путем:
Из того, что ![]() можно представить в следующем виде:
можно представить в следующем виде:
![]() ,
,
мы можем составить систему:
![]()
 ,
,
при этом значения ![]() заданы начальным условием;
заданы начальным условием;
Так как ![]() также известны, мы можем переписать систему линейных уравнений в матричном виде:
также известны, мы можем переписать систему линейных уравнений в матричном виде:
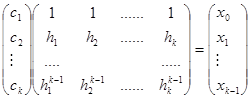
Отметим, однако, что поскольку 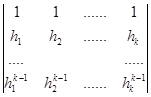 является определителем Вандермонда, то, как не трудно понять, он не будет равен нулю, если
является определителем Вандермонда, то, как не трудно понять, он не будет равен нулю, если ![]() – попарно различные.
– попарно различные.
Таким образом, получается, что у матрицы вида
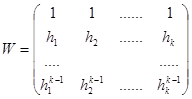 существует и, очевидно, единственная обратная матрица
существует и, очевидно, единственная обратная матрица ![]() и тогда вышеприведенное выражение примет следующий вид:
и тогда вышеприведенное выражение примет следующий вид:
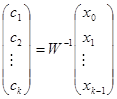 , отсюда
, отсюда ![]() находятся, причем однозначно.
находятся, причем однозначно.
Для рекуррентного соотношения, которому удовлетворяет последовательность ![]() , нам интересно получить выражение
, нам интересно получить выражение ![]() через
через ![]() в замкнутом виде. С помощью производящих функций эта задача решается в четыре шага, которые выполняются достаточно механически:
в замкнутом виде. С помощью производящих функций эта задача решается в четыре шага, которые выполняются достаточно механически:
· Записать одно уравнение, выражающее ![]() через другие элементы последовательности. Это уравнение должно оставаться справедливым для всех целых
через другие элементы последовательности. Это уравнение должно оставаться справедливым для всех целых ![]() с учетом того, что
с учетом того, что ![]() =
= ![]() .
.
· Умножить обе части уравнения на ![]() и просуммируйте по всем
и просуммируйте по всем ![]() . В левой части получится сумма
. В левой части получится сумма ![]() , которая равна производящей функции
, которая равна производящей функции ![]() . Правую часть следует преобразовать с тем, чтобы она превратилась в какое-то другое выражение, включающее
. Правую часть следует преобразовать с тем, чтобы она превратилась в какое-то другое выражение, включающее ![]() .
.
· Решить полученное уравнение, получив для ![]() выражение в замкнутом виде.
выражение в замкнутом виде.
· Разложить ![]() в степенной ряд и выписать отдельно коэффициент при
в степенной ряд и выписать отдельно коэффициент при ![]() ; это и будет замкнутый вид для
; это и будет замкнутый вид для ![]() .
.
Следующие две теоремы показывают, что приведенная схема достаточно универсальна, чтобы решить, в частности, любое линейное однородное рекуррентное уравнение с постоянными коэффициентами.
Теорема 1.
Пусть последовательность ![]() задается линейным однородным рекуррентным уравнением порядка
задается линейным однородным рекуррентным уравнением порядка ![]() с постоянными коэффициентами
с постоянными коэффициентами ![]() :
: ![]() , где числа
, где числа ![]() заданы.
заданы.
Тогда производящая функция ![]() – рациональна, то есть представима в виде отношения двух многочленов,
– рациональна, то есть представима в виде отношения двух многочленов, ![]() , причем степень многочлена Q равна
, причем степень многочлена Q равна ![]() , а степень многочлена P не превосходит
, а степень многочлена P не превосходит ![]() .
.
Доказательство:
Умножим производящую функцию ![]() на
на ![]() ,
,
получим

при ![]() из равенства
из равенства
![]()
Следовательно, по аналогии получаем:
![]() ,
,
то есть ![]() ,
,
где степень многочлена P не превосходит ![]() . Заметим, что многочлен Q имеет вид:
. Заметим, что многочлен Q имеет вид:
![]() .
.
Теорема 2.
Если производящая функция ![]() – рациональна,
– рациональна, ![]() , где многочлены P и Q взаимно просты, то, начиная с некоторого номера n, последовательность
, где многочлены P и Q взаимно просты, то, начиная с некоторого номера n, последовательность ![]() задается линейным рекуррентным соотношением:
задается линейным рекуррентным соотношением:
![]() , где k – степень многочлена Q , а
, где k – степень многочлена Q , а ![]() – некоторые константы.
– некоторые константы.
Из этих двух теорем мы получаем, что производящая функция ![]() последовательности, описываемой линейным однородным рекуррентным уравнением с постоянными коэффициентами, всегда представима в виде
последовательности, описываемой линейным однородным рекуррентным уравнением с постоянными коэффициентами, всегда представима в виде ![]() , где P и Q – некоторые многочлены. Полученную дробь мы можем разложить на простейшие, используя метод неопределенных коэффициентов, что мы и будем делать в представленных ниже примерах.
, где P и Q – некоторые многочлены. Полученную дробь мы можем разложить на простейшие, используя метод неопределенных коэффициентов, что мы и будем делать в представленных ниже примерах.
Определив главные понятия и освоив необходимую математическую технику, мы теперь можем перейти к рассмотрению того, как данный математический аппарат используется в экономических моделях.
Паутинообразная модель – одна из простейших экономических моделей, описывающих процесс ценообразования на некотором рынке и учитывающих эффект запаздывания. В данной модели принимается во внимание то, что при планировании объемов рыночной сделки, потребители и производители могут оказаться в неодинаковом положении. Покупатель, планируя в периоде t объем спроса, знает цену в этом периоде, а производитель в момент осуществления мероприятий, определяющих объем его предложения, не имеет представления, какова будет цена к моменту выхода продукции на рынок. Так, фермер, определяя площади посева, не знает цену урожая в день его реализации; когда производитель мебели определяет объем ее выпуска, ему еще неизвестно, по какой цене ее можно будет продать. В паутинообразной модели ценообразования предполагается, что ожидаемая производителями в периоде t цена в период t+1 равна текущей цене. Иначе говоря, производитель принимает сегодня решение об объеме продаж завтра на основе сегодняшней цены. Таким образом, в паутинообразной модели объем рыночного спроса в периоде t зависит от цены этого периода: ![]()
![]() , а объем рыночного предложения в данном периоде определяется ценой предшествовавшего периода:
, а объем рыночного предложения в данном периоде определяется ценой предшествовавшего периода: ![]() , где
, где ![]() – некоторые коэффициенты. При этом мы будем рассматривать лишь случай, когда
– некоторые коэффициенты. При этом мы будем рассматривать лишь случай, когда ![]() как экономически содержательный. При таком поведении рыночных агентов в любом периоде объем отраслевого спроса будет равен объему предложения, если
как экономически содержательный. При таком поведении рыночных агентов в любом периоде объем отраслевого спроса будет равен объему предложения, если ![]() .
.
![]()
пусть:
![]() и
и ![]() , тогда
, тогда ![]() (5)
(5)
введем новые обозначения:
![]()
![]() ,
,![]()
В новых обозначениях равенство (5) приобретает следующий вид: ![]()
![]()
n=1: ![]()
![]()
![]()
Таким образом, производящая функция ![]() последовательности
последовательности ![]() удовлетворяет тождеству
удовлетворяет тождеству
![]() ,
,
![]()
![]() ,
,
Случай, когда ![]() не возникнет, так как мы рассматриваем только те варианты, когда
не возникнет, так как мы рассматриваем только те варианты, когда ![]() как экономически содержательные.
как экономически содержательные.
Поэтому в общем случае ![]() и
и ![]() будет иметь вид:
будет иметь вид:
![]()
![]()
![]()
![]()
![]() =>
=> ![]()
![]()
![]()
![]()
![]() =>
=> ![]() и
и ![]()
![]()
вспомогательные вычисления:
![]() ,
, ![]()
![]()
![]() , возвращаясь к исходным обозначениям, получим следующее уравнение:
, возвращаясь к исходным обозначениям, получим следующее уравнение:
![]() . (6)
. (6)
Данное уравнение описывает процесс приспособления рынка к долгосрочному равновесию. Таким образом, результатом решения динамической модели отраслевого равновесия является не скаляр, а функция, описывающая изменение рыночной цены во времени.
Из равенства (6) следует, что последовательность цен ![]() сходится к равновесному состоянию
сходится к равновесному состоянию ![]() при любом начальном условии
при любом начальном условии ![]() (то есть равновесие
(то есть равновесие ![]() является глобально устойчивым) тогда и только тогда, когда
является глобально устойчивым) тогда и только тогда, когда ![]() , т.е. при |b| > n. Поскольку параметры b и n определяют углы наклона линий спроса и предложения, то долгосрочное равновесие в «паутинообразной» модели ценообразования является глобально устойчивым только в том случае, когда прямая спроса имеет меньший наклон к оси абсцисс, чем прямая предложения.
, т.е. при |b| > n. Поскольку параметры b и n определяют углы наклона линий спроса и предложения, то долгосрочное равновесие в «паутинообразной» модели ценообразования является глобально устойчивым только в том случае, когда прямая спроса имеет меньший наклон к оси абсцисс, чем прямая предложения.
Для наглядности, рассмотрим конкретные примеры.
Условие 1 задачи: На сельскохозяйственном рынке, где выполняются предположения паутинообразной модели, объем рыночного спроса и предложения имеют следующий вид:
,
.
Предположим, что долгосрочное равновесие было установлено в течение нескольких лет, но затем в один год произошли неожиданно хорошие урожаи и поэтому объемы производства повысились до 160. Выясним (используя полученное соотношение (6)), как цена будет вести себя в следующие годы после случившегося шока.
Цену в долгосрочном равновесии можно найти, приравняв объемы спроса и предложения:
=>
В задании говорится, что произошел скачок в предложении на уровень 160. Поэтому, когда цена корректируется, а продукция еще не продана,можно найти, подставив это значение в выражение спроса:
=>
.
![]()
![]() , подставляем вычисленные значения в полученную формулу (6)
, подставляем вычисленные значения в полученную формулу (6)
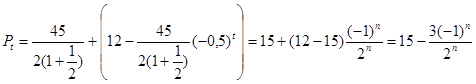
![]()
![]()
![]() – выполняется условие стабильности.
– выполняется условие стабильности.
Построим график (Рис. 1), для этого вычислим требующиеся значения:
В рассмотренном примере цена довольно быстро сходится к своему долгосрочному равновесию ![]() .
.
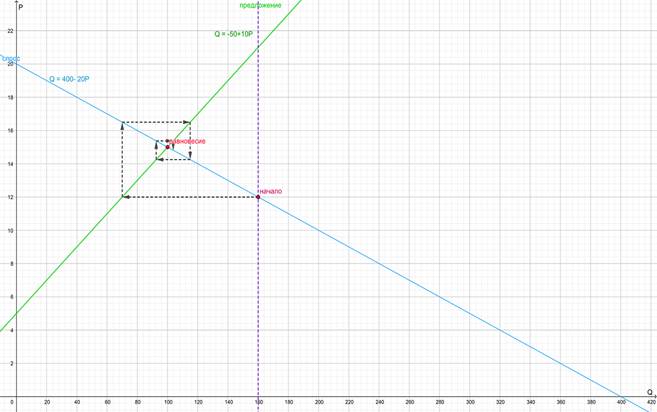
Рис. 1 Иллюстрация к задаче 1.
Условие 2 задачи: На сельскохозяйственном рынке, где выполняются предположения паутинообразной модели, объем рыночного спроса и предложения имеют следующий вид:
,
Долгосрочное равновесие было нарушено в связи с тем, что объемы производства изменились и стали равняться 90. Выясним, как будут вести себя цены в последующие годы.
Показатель цены при долгосрочном равновесии можно найти, приравняв объемы спроса и предложения:
=>
. Чтобы выяснить, какой станет цена при таком скачке, приравняем новое предложение к спросу:
![]()
![]()
![]() – нестабильное равновесие.
– нестабильное равновесие.
Построим график (Рис. 2) по следующим значениям:
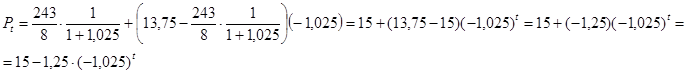
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – цена все еще находится около 13.
– цена все еще находится около 13.
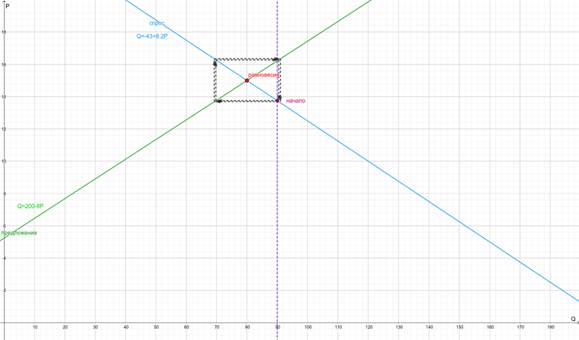
Рис. 2 Иллюстрация к задаче 2.
В двух предыдущих задачах мы рассмотрели случаи, когда ![]() и
и ![]() , возникает естественный вопрос: а что будет, когда
, возникает естественный вопрос: а что будет, когда ![]() ? Решим следующую задачу:
? Решим следующую задачу:
Условие 3 задачи. На сельскохозяйственном рынке, где выполняются предположения паутинообразной модели, объем рыночного спроса и предложения имеют следующий вид:
,
.
Предположим, что ранее господствующее долговременное равновесие нарушается неожиданно низким объемом производства в размере 50. Спрашивается, что произойдет с ценой в следующие периоды времени?
Заметим, что ![]() и
и ![]() Чтобы найти, какой станет цена при таком скачке, приравняем новое предложение к спросу:
Чтобы найти, какой станет цена при таком скачке, приравняем новое предложение к спросу:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, при t → ∞ ![]() не сходится к равновесному уровню, а колеблется между двумя уровнями цен из года в год.
не сходится к равновесному уровню, а колеблется между двумя уровнями цен из года в год.
Этот пример иллюстрирует случай, когда рынок и нестабильный, и неизменяющийся (Рис. 3).
Найдем цены:![]()
![]()
![]()
![]()
![]() и так далее.
и так далее.
![]()
![]()
![]()
![]()
![]()
![]() , все дальнейшие значения будут повторяться.
, все дальнейшие значения будут повторяться.
Цена колеблется между значениями 35 и 55.
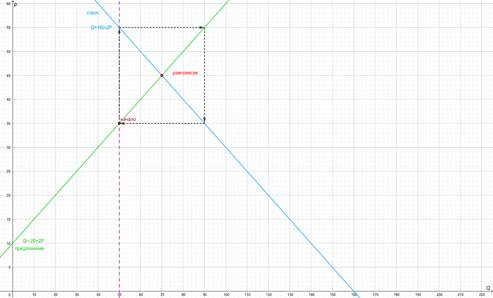
Рис. 3 Иллюстрация к задаче 3.
Перейдем к следующему примеру. В нем аппарат рекуррентных уравнений используется для описания динамики объема долговых обязательств.
Пусть ![]() является объемом задолженности в момент времени t. Тогда долг в последующий момент времени
является объемом задолженности в момент времени t. Тогда долг в последующий момент времени ![]() равен:
равен:
![]() ,
,
где![]() – процент, начисленный в конце периода t,
– процент, начисленный в конце периода t,![]() – сумма, идущая в счет погашения долга в момент времени t (данный платеж включает плату за процент и погашение основной суммы).
– сумма, идущая в счет погашения долга в момент времени t (данный платеж включает плату за процент и погашение основной суммы).
При этом для простоты будем считать процентную ставку r постоянной. Предположим, что первоначальный размер долга (в момент времени ![]() ) равен
) равен ![]() .Если выплачиваемые в счет погашения долга суммы
.Если выплачиваемые в счет погашения долга суммы ![]() постоянны и равны
постоянны и равны ![]() , как это часто бывает, тогда мы получим следующее рекуррентное уравнение:
, как это часто бывает, тогда мы получим следующее рекуррентное уравнение:
![]()
Введем новые обозначения: пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
тогда исходное уравнение примет следующий вид:
![]() . Найдем решение этого рекуррентного уравнен6ия с помощью аппарата производящих функций.
. Найдем решение этого рекуррентного уравнен6ия с помощью аппарата производящих функций.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Разложим рациональную дробь ![]() на простейшие, используя метод неопределенных коэффициентов:
на простейшие, используя метод неопределенных коэффициентов:
![]()
![]()
![]()
![]() =>
=> ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() ,
,
подставим полученные значения для ![]() и
и ![]() :
:
![]()
![]() , тогда, возвращаясь к исходным обозначениям, получим:
, тогда, возвращаясь к исходным обозначениям, получим:
![]() , а
, а ![]() .
.
Предположим теперь, что задолженность должна быть полностью погашена к началу периода ![]() , тогда можно рассчитать соответствующий постоянный платеж Z(платежи постоянные, пока
, тогда можно рассчитать соответствующий постоянный платеж Z(платежи постоянные, пока ![]() . Как только весь долг будет выплачен полностью, платежи прекращаются и с этого момента Z=0) , задав, что
. Как только весь долг будет выплачен полностью, платежи прекращаются и с этого момента Z=0) , задав, что ![]() , тогда
, тогда
![]()
![]() .
.
Откуда ![]() или
или ![]() .
.
Полученное выражение известно как формула для расчета размера аннуитета в финансовой математике и соответствует случаю постнумерандо без капитализации (см., например, [2 , раздел 7.6]). Заметим, что платеж Z, необходимый для погашения задолженности, уменьшается с ростом T. Обратим внимание на то, что при ![]()
![]() . В этом случае оплата (
. В этом случае оплата (![]() ) просто равна процентам, начисляемым в каждый период. Иными словами, долг никогда не возвращается и равен первоначальной задолженности
) просто равна процентам, начисляемым в каждый период. Иными словами, долг никогда не возвращается и равен первоначальной задолженности ![]() в каждом периоде. Если же
в каждом периоде. Если же ![]() , то долг погашается за конечный период времени. Предположим, что вместо того, чтобы требовать, что долг должен быть равен нулю в некоторое время (в том числе и при
, то долг погашается за конечный период времени. Предположим, что вместо того, чтобы требовать, что долг должен быть равен нулю в некоторое время (в том числе и при ![]() ), мы наложим условие на то, чтобы настоящая дисконтированная стоимость долга была бы неположительной по мере того, как T приближается к бесконечности:
), мы наложим условие на то, чтобы настоящая дисконтированная стоимость долга была бы неположительной по мере того, как T приближается к бесконечности:
![]() Выполнение этого условия (известного как no Ponzi game condition, NPG) гарантирует невозможность реализации схемы финансовой пирамиды, в которой основные выплаты и процентные платежи оплачиваются путем выпуска нового долга.
Выполнение этого условия (известного как no Ponzi game condition, NPG) гарантирует невозможность реализации схемы финансовой пирамиды, в которой основные выплаты и процентные платежи оплачиваются путем выпуска нового долга.
Действительно, если вышеуказанное выражение будет положительным, то заемщик сможет извлекать средства от кредиторов.
NPG условие с постоянной выплатой эквивалентно следующему выражению:
Или, что тоже, ![]() . Таким образом, условие NPG выполняется, если размер выплачиваемой в счет погашения долга суммы Z не меньше, чем процент. Наряду с дифференциальными уравнениями, разностные (рекуррентные) уравнения представляют собой один из основных подходов к описанию экономической динамики. Настоящую работу следует рассматривать как первый шаг в освоении данного подхода.
. Таким образом, условие NPG выполняется, если размер выплачиваемой в счет погашения долга суммы Z не меньше, чем процент. Наряду с дифференциальными уравнениями, разностные (рекуррентные) уравнения представляют собой один из основных подходов к описанию экономической динамики. Настоящую работу следует рассматривать как первый шаг в освоении данного подхода.
Список используемой литературы:
1. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики: Пер. с англ. — М.: Мир, 1998.
2. Ковалев В.В. Введение в финансовый менеджмент. М., 2006.
3. Ландо С. К. Лекции о производящих функциях. — 2-е изд., испр. — М.: МЦНМО, 2004. — 144 с.
4. Романко В. К. Разностные уравнения. М., 2015.
5. Тарасевич Л.С., Гребенников П.И., Леусский А.И. Микроэкономика: Учебник. 4-е изд., испр. и доп. — М.: Юрайт_Издат, 2006. — 374 с.
6. Neusser K. Difference Equations for Economists. 2016. Unpublished manuscript. http://www.neusser.ch/downloads/DifferenceEquations.pdf
7. Rosser M. Basic mathematics for economists. London, 2003.

