Структурированная кабельная система (СКС) — универсальная телекоммуникационная система здания, организации, предназначенная для поддержки функционирования широкого круга приложений, таких как компьютерные, телевизионные и телефонные сети, системы видеонаблюдения, системы пожарной и охранной сигнализаций и т.д.
На сегодняшний день явно видна тенденция замены электрических кабелей связи на оптоволоконные кабели, однако медножильные кабели не теряют своей актуальности и нашли широкое применение именно в СКС. Наряду с преимуществами оптических волокон, существуют и недостатки. При планировании сетей внутри зданий необходимо выдерживать требуемый радиус изгиба оптоволокна, что довольно сложно реализовать. Также стоит отметить высокую стоимость интерфейсного оборудования — оптических приемников и передатчиков. Данные недостатки ограничивают использование кабелей на основе оптических волокон при построении новых и модернизации существующих кабельных систем и сетей.
Медножильные кабели связи остаются актуальны не только в горизонтальной, но и магистральной подсистемах структурированных кабельных систем, в которых активно применяется технология xDSL, в качестве среды передачи использующая симметричные кабели связи, изготовленные по технологии витой пары. Их спецификация представлена в ГОСТ Р 53246-2008 [1]. В данной статье речь пойдет о кабеле 5 категории UTP с рабочим диапазоном частот до 100 МГц, используемому в магистральной подсистеме СКС.
Объемы данных, передаваемых в кабельных сетях, с каждым годом возрастают, следовательно, ужесточаются и требования, предъявляемые к кабелям связи по их электрическим характеристикам, пропускной способности и передаваемым полосам частот.
Электромагнитное влияние между цепями в цифровых системах передачи на основе симметричных кабелей является одним из главных источников помех, ограничивающих длины регенерационных участков ЦСП. На правильность принятия решения регенератором влияет соотношение мгновенных значений сигнал/помеха в момент появления стробирующего импульса. Следовательно, для определения оптимальных длин регенерационного участка необходимо знать закон изменения мгновенного значения помехи, определяемой влиянием между цепями.
Таким образом, в связи с возрастающими требованиями, предъявляемыми к симметричным кабелям, которые позволяют обеспечить передачу сигналов всех типов, включая речевые, информационные, видео, является актуальной задача теоретически и экспериментально исследовать взаимные электромагнитные влияния между симметричными цепями кабеля.
В работе [2] показано, что взаимные электромагнитные влияния между симметричными цепями на ближний конец (БК) в большей части обуславливает непосредственный переход энергии между цепями, подверженными влиянию.
В зависимости от конструкции кабелей электромагнитные влияния между цепями могут происходить за счет систематической регулярной (при идеальной симметрии цепей) и нерегулярной (вследствие отклонения конструкции взаимовлияющих цепей от идеальной) составляющих электромагнитных связей.
При систематической (равномерно распределенной по длине) связи между цепями передаточная функция влияния имеет вид:
(1)
где
;
;
;
;
; 
; 
;
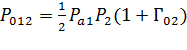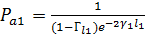– передаточная функция, описывающая электромагнитные влияния между регулярными согласованными цепями;
,
– передаточные функции, описывающие дополнительное влияние, обусловленное несогласованностью взаимовлияющих цепей;
–коэффициенты отражения на выходе первой и второй цепей:
– коэффициент отражения на входе второй цепи:
– коэффициенты распространения первой и второй цепей;
– длины соответствующих цепей;
– оператор Лапласа; 
– круговая частота.
Для случая согласованных цепей передаточные функции 
, а выражение принимает вид
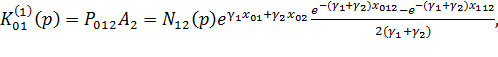(2)
где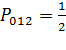 
, 
– коэффициент электромагнитной связи на БК;
, 
– координата начала первой и второй цепей.
Приняв 
; 
, 
– длина СЦ. После преобразований (2) получим:
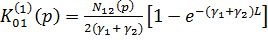(3)
Так как в симметричных кабелях связи активные составляющие электромагнитных связей пренебрежимо малы, поэтому коэффициент электромагнитной связи на БК определяется в основном реактивной составляющей связи 
.
После подстановки в (3) имеем:
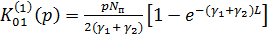(4)
Тогда при систематической связи частотная характеристика переходного затухания на БК между СЦ:
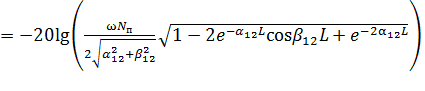(5)
где 
– коэффициент затухания 1-й и 2-й цепей, дБ/км;
– коэффициент фазы 1-й и 2-й цепей, рад/км.
На основе формулы (5) был проведен расчет для двух длин кабеля и получен график 
(рис. 1), имеющий волнообразный характер. Для расчета было использовано значение электромагнитной связи близкое к реальному и полученное экспериментальным путем 
.
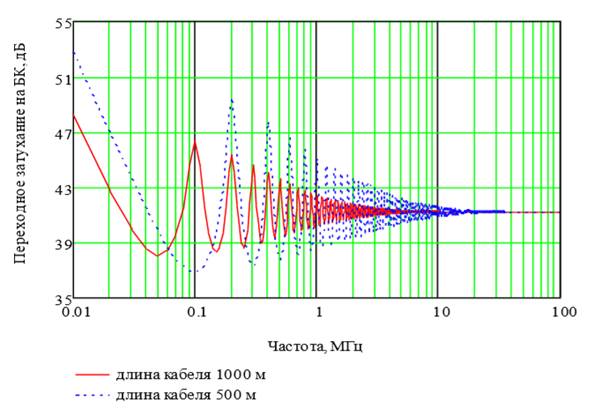
Рис. 1. График для двух длин кабелей UTP cat 5
Длины кабелей, взятых для расчета – 500 и 1000 метров. Анализ представленных графиков показал, что для кабеля длиной 500 метров характеристика переходного затухания имеет осцилляции приблизительно до 20 МГц, для кабеля длиной 1000 метров – до 5МГц, а далее с увеличением частоты они сглаживаются. Уменьшение длины линии приводит к увеличению значения переходного затухания на БК, чего и следует добиваться на практике. Данный расчет справедлив лишь для случая, когда к концам взаимовлияющих цепей включены согласованные нагрузки, и из формулы (1) достаточно учесть только первое слагаемое суммы, так как малая асимметрия цепи не влияет на параметры ее передачи.
Чаще на практике возникает необходимость учета несогласованности цепей. Их асимметрия может привести к значительному увеличению взаимных влияний между цепями ЛС, так как появившиеся на концах цепи отраженные сигналы создают помеху полезному сигналу. Тогда при анализе взаимных электромагнитных влияний необходимо учесть составляющие 
Согласно [3] симметричные кабели связи для цифровых систем передачи, предназначенные для эксплуатации в СКС, имеют разные шаги скрутки цепей. В этом случае наряду с регулярной составляющей электромагнитной связи необходимо учитывать и нерегулярную 
, где 
– функция, учитывающая случайный характер изменения связей по длине волны. В [5] доказано, что случайный характер нерегулярной составляющей на основании предельной теоремы Ляпунова позволяет заменить ее стационарной функцией. Для математического описания 
целесообразно использовать вероятностные характеристики – дисперсией 
и нормированную автокорреляционную функцию 
.
Для нерегулярной составляющей электромагнитной связи электромагнитное влияние на ближний конец можно охарактеризовать количественно с помощью среднего значения квадрата модуля передаточной функции влияний 
и среднего значения переходного затухания 
.
В работе [4] показано, что
, (6)
где 
– автокорреляционная функция случайной функции .
Автокорреляционную функцию 
можно найти, зная аппроксимирующую функцию нормированной автокорреляционной функции . В [2] рассмотрены несколько выражений, которыми могут быть аппроксимированы автокорреляционные функции в симметричных кабелях связи. Так как при расчете кабельных ЛС часто используются стационарные случайные функции, представляющие собой отрезки одинаковой длины (такие как скрученные участки цепей, подверженных влиянию) с постоянными по длине связями, то для аппроксимации подойдет линейная автокорреляционная функция
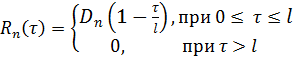(7)
С учетом, что и подставив (7) в выражение (6), после преобразований получим
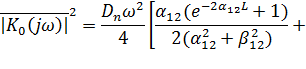
(8)
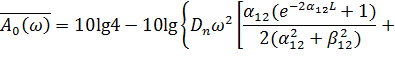
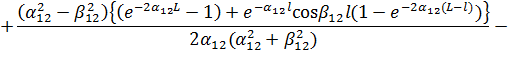
, (9)
где 
– интервал корреляции нормированной автокорреляционной функции .
Именно он во много определяет величину переходного затухания. – интервал корреляции подбирается экспериментально для конкретной конструкции кабеля.
С использованием формулы (9) был построен график переходного затухания на ближний конец для нерегулярной составляющей электромагнитной связи (рис.2). При расчетах были взяты два значения интервала корреляции, 12мм – минимальный шаг скрутки исследуемого кабеля, а 47 мм –максимальный.
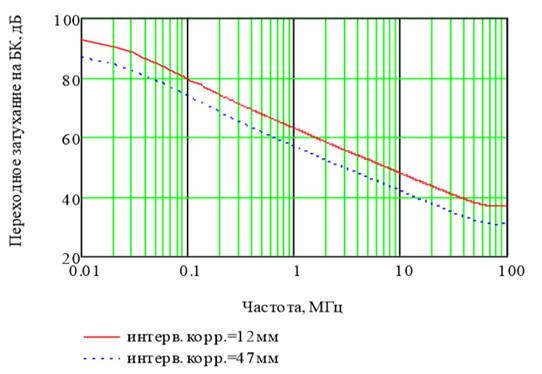
Рис. 2. Графики
для двух длин шага скрутки кабеля UTP cat 5
Значение дисперсии нерегулярной составляющей связи было получено экспериментальным путем и равно 
(с/км)2. Из анализа представленных графиков видно, что переходное затухание на БК монотонно убывает, а также при увеличении интервала корреляции снижается во всем спектре частот.
В общем случае, изменение электромагнитной связи по длине линии представляется как
В (10) учтена как систематическая 
составляющая связи, так и несистематическая , имеющая случайный характер. В случае преобладания систематической составляющей передаточная функция влияния 
описывается выражением (3). Если же нерегулярная составляющая оказывает большее влияние, тогда 
следует рассчитывать по (8). В общем случае суммарное электромагнитное влияние определяется как
, (11)
После подстановки (3) и (4) в (11) получим
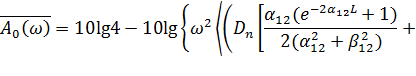
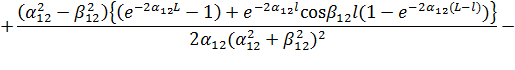
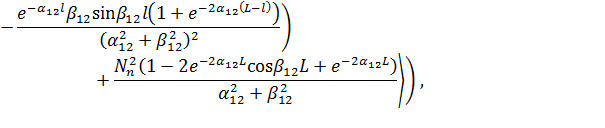
(12)
В соответствии с выражением (12) на рис. 3 представлены графики суммарного переходного затухания на БК для двух длин интервала корреляции.
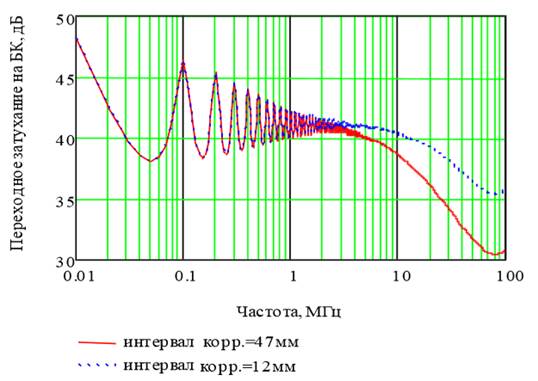
Рис. 3. Графики суммарного для двух длин шага скрутки кабеля
UTP cat 5
При расчетах использовались следующие исходные данные:
(с/км)2, 
, 
м. Из рис. 3 видно, что до 5 МГц оказывает влияние систематическая составляющая электромагнитной связи, а после 5 МГц – нерегулярная. С увеличением интервала корреляции (шага скрутки) снижается значение переходного затухания на ближний конец в высокочастотной области.
Зависимость суммарного переходного затухания на БК от длины волны представлена на рис. 4. Для расчетов были взяты длины кабеля 500 и 1000 м, шаг скрутки одинаков – 12 мм.
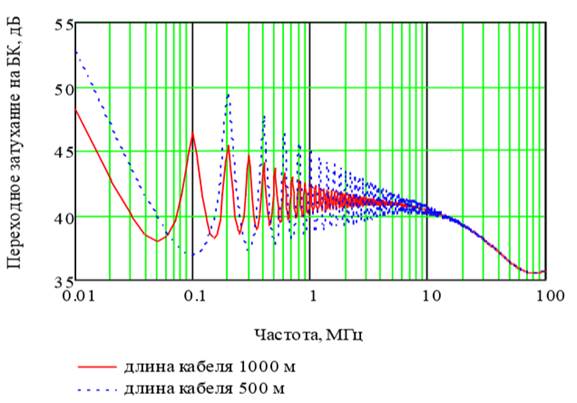
Рис. 3. Графики суммарного для двух длин кабеля UTP cat 5
Анализ графиков показывает, что длина кабеля определяет значение суммарного переходного затухания на БК в области частот до 5 МГц и 20 МГц для кабелей длиной 1000 и 500 м соответственно, где определяющим является закон изменения систематической составляющей электромагнитной связи. С ростом частоты графики совпадают.
Таким образом, рассмотренная математическая модель показала, что в симметричных кабелях электромагнитные влияния складываются из систематической (для относительно низкого диапазона частот) и нерегулярной (присущей высокочастотной области) составляющей электромагнитных связей. Увеличивая длину линии, можно добиться уменьшения осцилляций и увеличения переходного затухания на БК в области низких частот. В высокочастотной области того же эффекта можно достичь, изменяя шаг скрутки цепей.
Грамотный подбор параметров симметричного кабеля позволяет снизить электромагнитные влияния между цепями и повысить качество передачи информации.
ЛИТЕРАТУРА
1. ГОСТ Р 53246-2008. Информационные технологии. Системы кабельные структурированные. Проектирование основных узлов системы. Общие требования. – Москва: Изд-во стандартов, 2010. – 84 с.
2. Андреев В.А. Временные характеристики кабельных линий связи. –
М.: Радио и связь,1986. – с. 45-49.
3. Андреев В.А., Андреев Р.В, Попов В.Б. Электромагнитные влияния между цепями кабелей внутриобъектовой связи и широкополосного доступа. Монография. — Самара.: ФГБОУВО ПГУТИ, 2017. – с. 189-202.
4. ГОСТ Р 54429-2011. Кабели связи симметричные для цифровых систем передачи. Общие технические условия. – Москва: Изд-во стандартов, 2012. – 46 с.
5. Левин Б.Р. Теоретические основы статистической радиотехники.
Кн. 1. – М.: Сов. радио, 1974. – с. 98.
1. GOST R 53246-2008. Informacionnye tehnologii. Sistemy kabel’nye strukturirovannye. Proektirovanie osnovnyh uzlov sistemy. Obshhie trebovanija. – Moskva: Izd-vo standartov, 2010. – 84 s.
2. Andreev V.A. Vremennye harakteristiki kabel’nyh linij svjazi. – M.: Radio i svjaz’,1986. – s. 45-49.
3. Andreev V.A., Andreev R.V, Popov V.B. Jelektromagnitnye vlijanija mezhdu cepjami kabelej vnutriob#ektovoj svjazi i shirokopolosnogo dostupa. Monografija. — Samara.: FGBOUVO PGUTI, 2017. – s. 189-202.
4. GOST R 54429-2011. Kabeli svjazi simmetrichnye dlja cifrovyh sistem peredachi. Obshhie tehnicheskie uslovija. – Moskva: Izd-vo standartov, 2012. – 46 s.
5. Levin B.R. Teoreticheskie osnovy statisticheskoj radiotehniki. Kn. 1. – M.: Sov. radio, 1974. – s. 98.
