Занимаясь изучением краевых задач доктрины функций в бесконечных областях [2] довольно нередко появляется надобность применения пространств функций, которые бы удовлетворяли условию Гёльдера по отношению к метрике сферы Римана [1].
Определение. Одноточечная компактификация ![]() евклидового пространства
евклидового пространства ![]() есть метрика сферы Римана.
есть метрика сферы Римана.
Согласно определению, окрестностями элемента ![]() в этой операции, преобразующей топологические пространства в компактные будут служить дополнения к шарам. Более того, непрерывность функции
в этой операции, преобразующей топологические пространства в компактные будут служить дополнения к шарам. Более того, непрерывность функции ![]() в точке
в точке ![]() означает существование предела
означает существование предела ![]() . При
. При ![]() стереографическая проекция устанавливает гомеоморфизм компакта
стереографическая проекция устанавливает гомеоморфизм компакта ![]() на единичную сферу
на единичную сферу ![]() трехмерного пространства и поэтому компакт носит название сферы Римана. Отметим, собственно, что подобную проекцию можно установить и для
трехмерного пространства и поэтому компакт носит название сферы Римана. Отметим, собственно, что подобную проекцию можно установить и для ![]() , что означает сохранность введенного термина и в данном случае [1].
, что означает сохранность введенного термина и в данном случае [1].
Очевидно, инверсия
![]() (1)
(1)
относительно сферы ![]() с центром в точке
с центром в точке ![]() осуществляет гомеоморфизм компакта
осуществляет гомеоморфизм компакта ![]() на себя, причем
на себя, причем ![]() и
и ![]() . При
. При ![]() это преобразование будем обозначать
это преобразование будем обозначать ![]() . Заметим, что оно переставляет точки
. Заметим, что оно переставляет точки ![]() ,
, ![]() и взаимно обратно. Обратным к (1), в общем случае, является преобразование
и взаимно обратно. Обратным к (1), в общем случае, является преобразование ![]() .
.
Компакт ![]() можно наделить естественной структурой метрического пространства. С этой целью с каждой парой его точек
можно наделить естественной структурой метрического пространства. С этой целью с каждой парой его точек ![]() свяжем неотрицательное число
свяжем неотрицательное число ![]() по формуле
по формуле
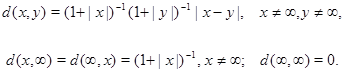
Заметим, что тогда ![]() при
при ![]() .
.
Лемма. Функция ![]() есть расстояние. Инверсия, заданная формулой (1), относительно функции
есть расстояние. Инверсия, заданная формулой (1), относительно функции ![]() удовлетворяет следующей двусторонней оценке:
удовлетворяет следующей двусторонней оценке:
![]()
Доказательство. Чтобы доказать первое утверждение леммы проверим выпонимость неравенства треугольника для трех точек ![]() . Заметим, собственно, что это неравенство уточняется непосредственно, когда одна из данных точек совпадает с
. Заметим, собственно, что это неравенство уточняется непосредственно, когда одна из данных точек совпадает с ![]() [2]. Поэтому нужно доказать неравенство
[2]. Поэтому нужно доказать неравенство ![]() или, что равносильно, неравенство
или, что равносильно, неравенство ![]() Достаточно убедиться, что
Достаточно убедиться, что ![]() . Данное неравенство очевидно, если одна из точек
. Данное неравенство очевидно, если одна из точек ![]() совпадает с
совпадает с ![]() . В общем случае после деления на
. В общем случае после деления на ![]() оно переходит в
оно переходит в ![]() где положено
где положено ![]() и аналогично обозначение принято и для
и аналогично обозначение принято и для ![]() . Так как
. Так как
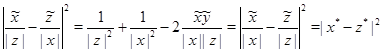 , аналогично для остальных пар точек, это неравенство совпадает с неравенством треугольника по отношению к евклидовой метрики. Перейдем к доказательству второго утверждения леммы, которое базируется на равенстве
, аналогично для остальных пар точек, это неравенство совпадает с неравенством треугольника по отношению к евклидовой метрики. Перейдем к доказательству второго утверждения леммы, которое базируется на равенстве
![]() (2)
(2)
Заметим, что равенство (2) равносильно следующему равенству:![]() Левая часть этого выражения равна
Левая часть этого выражения равна ![]() что совпадает с его правой частью. В силу (1), (2) расстояние
что совпадает с его правой частью. В силу (1), (2) расстояние ![]() можем записать в виде
можем записать в виде
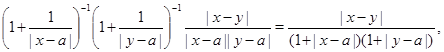
откуда ![]() где
где ![]() Остается заметить, что в силу очевидного неравенства
Остается заметить, что в силу очевидного неравенства ![]() выполнена оценка
выполнена оценка ![]() .
.
Определение. Условие Гёльдера [3] вводится и для функций, которые заданны на произвольном метрическом пространстве, по отношению к его метрике ![]() . Для этого нужно лишь заменить выражение
. Для этого нужно лишь заменить выражение ![]() в условии
в условии ![]() на выражение
на выражение ![]() . Соответствующий класс обозначим через
. Соответствующий класс обозначим через
![]() , указывая при необходимости метрику.
, указывая при необходимости метрику.
Как показано в [3] это пространство является банаховым относительно нормы ![]() .
.
Можно также ввести класс ![]() отображений
отображений ![]() из метрического пространства
из метрического пространства ![]() в
в ![]() с помощью условия Гельдера
с помощью условия Гельдера ![]()
Отметим, собственно, что все основные свойства нормированных пространств и теорема об эквивалентности общепризнанных мер в банаховых пространствах сохраняют свою силу и в данном случае, поскольку при их доказательстве специфика евклидового расстояния никак не применялась.
Использованные источники
1. Ковалёва Л. А., Чернова О. В. Математика как неотъемлемая компонента образования инженера-специалиста // Наука и образование: отечественный и зарубежный опыт. Сборник трудов конференции Двадцать третьей международной научно-практической конференции. – 2019. – С. 116-120.
2. Мусхелишвили Н. И. Сингулярные интегральные уравнения. – М.: Наука, 1968. – 511 с.
3. Солдатов А. П. Сингулярные интегральные операторы и эллиптические краевые задачи. I / А. П. Солдатов // СМФН. – 2017. – Т. 63, № 1. – С. 1–189.

