Введение
Важным
процессом разработки ракетных двигателей твердого топлива (РДТТ) и любых
двигательных установок (ДУ) – является математическое моделирование рабочих
процессов, происходящих внутри него. Разработка простых математических моделей
является перспективным направлением научных работ, т.к. позволяет существенно
повысить скорость работ и снизить их стоимость на начальном этапе
проектирования.
В
рамках проведенной работы была реализована математическая модель расчета внутрибаллистических
характеристик ракетного двигателя на твердом топливе, а также методика
построения профилированного сопла. Методика расчета внутрибаллистических
характеристик также может применяться в комбинированных ракетных двигателях на
твердом топливе (КРПД-Т) при расчете маршевого газогенератора.

Рисунок 1
Расчет
внутрибаллистических характеристик РДТТ
На
этапе проектирования, при термодинамических расчетах прибегают к модели
равновесного состояния продуктов сгорания. При наличии конденсированных фаз в
продуктах сгорания топлива поток условно рассматривается как газ, подчиняющийся
уравнению состояния идеального газа (1) с введением поправки в газовую
постоянную (2).
![]() (1)
(1)
![]() , (2)
, (2)
где z
– массовая доля всех конденсированных фаз.
Система
уравнений внутренней баллистики для камеры сгорания газогенератора:
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
где,
(3) – уравнение баланса массы,
(4)
– уравнение баланса энергии,
(5)
– уравнение изменения свободного объема,
(6)
– изменение свода горения.
Используя
уравнение состояния идеального газа (1) найдем массу продуктов сгорания в
камере газогенератора.
![]() (7)
(7)
– газоприход с поверхности заряда;
![]() (8) –
(8) –
расход продуктов сгорания через сопло;
![]() (9)
(9)
– внутренняя энергия продуктов сгорания;
![]() (10)
(10)
– энтальпия продуктов сгорания;
![]() (11)
(11)
– энтальпия маршевого топлива.
Подставляя
эти выражения в уравнения (3), (4), (5) и (6) получим систему дифференциальных
уравнений:
 (12)
(12)
![]() (13)
(13)
– комплекс-функция A(γ)
![]() (14)
(14)
– закон горения твердого топлива
![]() (15) –
(15) –
коэффициент в законе горения
Зависимости
термодинамических характеристик продуктов сгорания твердого топлива ![]() ,
, ![]() ,
, ![]() находятся в
находятся в
результате термодинамического расчета равновесного состояния.
Система
дифференциальных уравнений (12) имеет 4 начальных условия. Для определения
первого ![]() запишем уравнение
запишем уравнение
баланса массы (3) для стационарного процесса в начальный момент времени,
производная по времени равна нулю, поэтому:
![]() (16)
(16)
Из
полученного уравнения не удается явно выразить ![]() , т.к. R,
, т.к. R,
T и γ сами являются функциями давления, но решение может быть
найдено численно.
Остальные
начальные условия свода горения, начального свободного объема и температуры
имеют вид:
![]()
![]() (17)
(17)
![]()
Результаты
численного решения системы дифференциальных уравнений (12) представлен на
рисунках 2 и 3. Решение получено методом Эйлера, реализованным в среде MatLAB.

Рисунок 2

Рисунок 3
Результаты
внутрибаллистического расчета ракетного двигателя твердого топлива используются
далее для моделирования оптимального профиля сопла в заданных геометрических
ограничениях.
Моделирование
оптимального профиля сопла Лаваля
Геометрическими
ограничениями являются:
длина
сопла – l
радиус
среза – R1
критический
радиус – Rкр
Моделирование
профиля сопла состоит из трех участков (рис. 4):
1-2:
профиль сверхзвуковой части сопла
4-3:
дозвуковая часть
3-1:
переход с критики
3:
критическое сечение
1:
начало профилирования сопла

Рисунок 4
Переход
дозвуковой части на критическое сечение и с критического сечения на профиль
сверхзвуковой части сопла строится окружностями, центры которых лежат на одной
линии в плоскости критики (точка 3). На участке 3-1 радиус скругления берется
из отношения ![]() , а на участке 4-3
, а на участке 4-3
из ![]() .
.
Координаты
точки 1 высчитываются из уравнений:
 (18)
(18)
Углы
наклона касательной к параболе θ
берутся из графика (рис. 5)
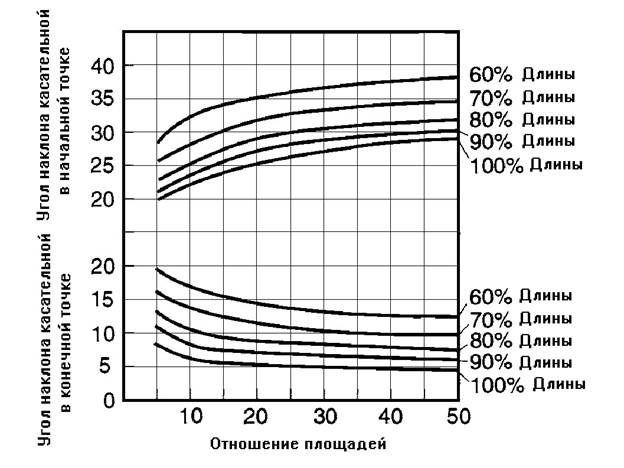
Рисунок 5
Длина
профилированного сопла берется как часть длины эквивалентного конического сопла
с полууглом раструба = 15о. Длина эквивалентного конического сопла
считается по формуле:
![]() (19)
(19)
Сама
профилированная часть сопла представляет собой параболу и строится по формуле:
![]() (20)
(20)
Коэффициенты
для построения параболы:
![]()
![]() (21)
(21)
![]()
Профилирование
сопла реализовано в среде MatLab,
представлен пример работы программы (рис. 6):
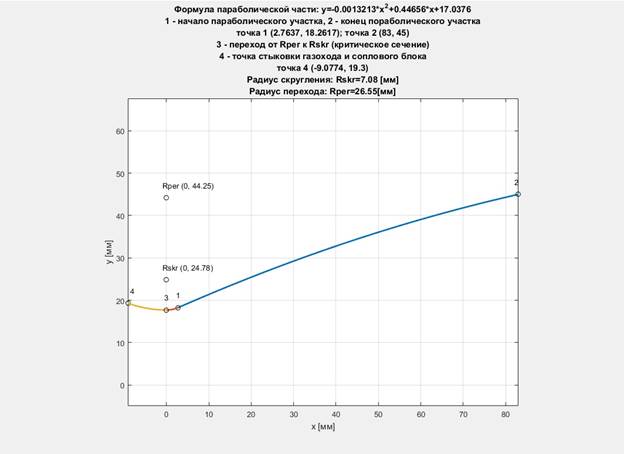
Рисунок
6
Сопло
построенное по результатам работы программы (рис. 7):
Рисунок 7
Таким
образом, представленная методика расчета ракетного двигателя твердого топлива и
проектирования оптимальной геометрии профилированного сопла позволяет
определить:
–
внутрибаллистические характеристики двигателя;
–
координаты точек обвода сопла.
Литература
1.
«РПД на твердых и пастообразных топливах»
– Сорокин В.А., Яновский Л.С., Козлов В.А., Москва ФИЗМАТЛИТ 2010г.
2.
«Интегральные ПВРД на твердых топливах» – Александров
В.Н., Быцкевич В.М., Верхоломов В.К., Москва ИКЦ «АКАДЕМКНИГА» 2006г.
3.
«Течения газа в соплах» – Пирумов У.Г.,
Росляков Г.С., Издательство Московского университета 1978г.
4.
«Recent
developments in rocket nozzle configurations» – RAO G.V.R., National
engineering science Co. Pasadena, Calif.
5.
«Rocket
Propulsion Elements» – George P. Sutton, A Wiley-Interscience Publication, 2001

