Первоначально
геометрические построения и задачи на построение, как отмечает Г.Х. Воистинова
[2, с. 40], были введены в школьную практику в связи с методической идеей об
использовании в обучении геометрии наглядности, практических работ,
геометрических построений во второй половине XIX века.
Как и в традиционной методике, задачей на построение
будем считать «математическое предложение, указывающее по каким данным, какими
средствами (инструментами) и какой геометрический образ (точка, прямая,
окружность, треугольник, совокупность точек и так далее) требуется найти
(начертить, построить на плоскости, наметить на местности и так далее) так,
чтобы этот образ удовлетворял определенным условиям» [Цит. по 2, с. 58].
Таким образом, сущность задач на построение не
исчерпывается указанием данных и формулировкой того, что требуется найти.
Важное значение имеет также указание на те средства, с помощью которых задача
должна быть решена, на те инструменты, при помощи которых построение должно
быть выполнено. В качестве основных инструментов в задачах на построение
принято считать циркуль и линейку (одностороннюю).
В школьной практике
наиболее используемыми методами решения задач на построение циркулем и
линейкой являются: геометрические преобразования и так называемый метод
геометрических мест точек.
Алгебраический метод решения
задач на построение циркулем и линейкой является одним из
методов решения практических задач. Именно с помощью
данного метода решаются вопросы, которые связаны
с решением задач тем или иным инструментом.
С помощью линейки можно провести произвольную прямую и отрезок, а
циркулем – окружность, имеющую произвольный радиус.
Этот метод так же позволяет решать много
сложнейших задач и хорошо выражает связь между алгеброй и
геометрией.
Однако в школьных учебниках алгебраическому методу
геометрии практически не уделяется внимание, хотя изучение этого метода не вызывает особых осложнений.
Под сущностью этого метода понимаются
следующие шаги:
а) задача сводится к построению отрезка;
б) применяя известные геометрические взаимоотношения искомых и данных, формируется равенство, выражающее их взаимосвязь;
в) с помощью решения уравнения находится длина отрезка;
г) по длине строится отрезок;
д) с помощью найденного отрезка строится
искомая фигура.
Как считают Б.И. Аргунов и М.Б. Балк [1, c
269], предварительная работа – это анализ ключевых формул
и способов построения, которые также выполняют отдельные компоненты схемы
решения задач алгебраическим методом, и применяют идею подобного расклада к решению задач.
В учебниках геометрии изучают построения циркулем
и линейкой отрезков, заданных с помощью следующих формул:
1) ![]() (Рис.
(Рис.
1).
2)![]() (Рис.
(Рис.
2).

Рис.
1 Рис. 2
3) ![]() ,
,
где n – натуральное число (Рис. 3).

Рис.
3 Рис. 4
4) ![]()
Построим луч данного отрезка «а» под произвольным углом
к нему. Откладываем на луче n раз произвольный отрезок b, так что OB = nb (Рис.
4). Соединяем точку В со вторым концом А отрезка а. Через точку В1,
определяемую условием ОВ1= b, проводим прямую,
которая параллельна АВ, и отмечаем точку A1–
пересечения отрезка а.
5) ![]() (построение отрезка,
(построение отрезка,
четвертого пропорционального трем данным отрезкам).
Запишем условие в виде с : а = b
: х. Пусть ОА = а, ОС = с (Рис. 5), так что члены одного из отношений отложены на луче,
исходящем из точки О. На другом луче, исходящем из этой же точки,
откладываем известный член другого отношения ОB = b. Через
точку А проводим некоторую прямую, параллельную ВС,
и отметим точку X – пересечения с прямой ОВ. Отрезок ОХ искомый,
то есть ОХ = х.
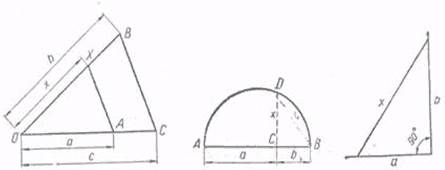
Рис. 5
Рис. 6 Рис. 7
7) ![]() (построение среднего
(построение среднего
пропорционального двух отрезков).
Построим отрезки АС и ВС, равные aи bсоответственно, так что АВ = а + b.
На АВ строим полуокружность (Рис. 6). От точки С отпустим перпендикуляр к АВ и
точку пересечения с окружностью обозначимD. Тогда х = CD.
8) ![]() . Отрезок x строится как гипотенуза
. Отрезок x строится как гипотенуза
прямоугольного треугольника, имеющего катеты а и b (Рис.
7).
9)![]() (a > b). Отрезок x строится
(a > b). Отрезок x строится
как катет прямоугольного треугольника с гипотенузой а и
катетом b.
К данным построениям можно свести
построения отрезков, заданных более сложными
формулами.
Рекомендуем исследовать эти формулы, когда
каждая из них рассматривается при анализе соответственного построения.
Здесь разумно также внедрение простых
задач на алгебраический метод (к примеру, задача о восстановлении
отрезков, если известны их сумма и разность) для того, чтобы продемонстрировать
их связь.
Рассмотрим задачу построения биссектрисы угла циркулем
и линейкой:
1.
Проведем окружность с центром в точке О произвольного радиуса,
которая пересечет стороны угла в точках Aи B.
2.
Проведем две окружности с центрами в точках Aи B одинакового радиуса. Они пересекутся в
точке С внутри угла AOB.
3.
Луч OC– биссектриса угла О.
Как отмечает Н.Ф. Четверухин [3, c. 147] не
всякая задача может быть решена с помощью циркуля и линейки. Еще в древности
греческие математики столкнулись с тремя задачами на построение, которые нельзя
было решить с помощью циркуля и линейки. И только через много лет были получены
их решения, которые основаны на теориях Галуа. Это задачи:
1. Удвоение объема куба – построение его
ребра с
объемом в два раза больше объема самого куба.
2. Трисекция угла – разделение
произвольного угла на три одинаковые части.
3. Квадратура круга – построение квадратас
площадью, равной площади круга.
Вывод. Описанные
методы рекомендуется использовать при решении
планиметрических задач на построение.
Ряд задач на построение может в одинаковой мере
решаться несколькими методами. И есть задачи, которые решаются комбинацией
основных построений.
Использованные
источники:
1.
Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости.
– М.: Учпедгиз, 1955. –269с.
2.
Воистинова
Г.Х. Задачи на построение как средство совершенствования приемов мышления
студентов: Монография. – Стерлитамак:Изд-во СФ БашГУ, 2013. – 184 с.
3.
Четверухин
Н.Ф. Методы геометрических построений. – М.:Учпедгиз, 1952. – 147с.

