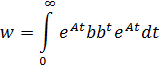Современная
теория систем автоматического управления использует, как известно, два типа
моделей – модели “вход-выход” и модели пространства состояний [1]. Первые ориентированы на
системы с одним входом и одним выходом, в то время как вторые позволяют решать
проблемы моделирования систем с несколькими входами и выходами. В первом случае
используется аппарат интегральных преобразований Лапласа и Фурье. Во втором —
аппарат теории матриц и дифференциальных управлений. Однако как в одном, так и
в другом случае ручные аналитические расчеты стали редкостью в связи с
появлением систем компьютерной математики. Самой известной и хорошо
приспособленной для решения задач управления является MATLAB фирмы MathWorks.
Она имеет специальные расширения Control Systens Toolbox и Simulink как раз для
моделирования систем управления. Однако MATLAB имеет одно, но весьма
существенное обстоятельство — ее высокая стоимость. Это исключает ее легальное
использование в большинстве технических университетов РФ.
В
предыдущей работе авторы обратили внимание на открытую систему Octave и
продемонстрировали ее применение для реализации частотных методов теории
управления [2]. В настоящей
работе показывается, что в Octave легко реализуются и методы пространства
состояний.
Octave является свободным программным
обеспечением, которое разрабатывается под лицензией GNU.
В настоящее время оно почти полностью совместимо с кодом MATLAB
и имеет различные преимущества. Самые главные из них — это свободное
распространение и доступность, а также низкие требования к производительности.
Это позволяет использовать Octave
в учебных заведениях, где отсутствует возможность приобрести лицензию MATLAB,
или характеристики используемых компьютеров не соответствуют требованиям для
работы с MATLAB.
Рассмотрим
задачу управления линейной стационарной системой с одним входом и одним
выходом, заданной своими уравнениями в пространстве состояний
|
|
|
(1) |
эта
система управляема, если
|
|
|
(2) |
или,
что эквивалентно, если не вырожден грамиан управляемости
|
|
|
(3) |
Рассмотрим
проверку свойства (2) и невыражденности грамиана (3) для передаточной функции
|
|
|
(4) |
Для
первой канонической формы в Octave записываем
|
>> |
A = [0 1; -6 -5]; |
|
>> |
b = [1; -3]; |
|
>> |
det( |
|
|
ans = |
|
|
0 |
Реализация
не является полностью управляемой. Количество неуправляемых координат – UNC –
находится так
|
>> |
UNC = length(A) – rank( |
|
|
UNC = |
|
|
1 |
Одна
координата — неуправляемая. Но если для той же передаточной функции
использовать управляемую форму, то реализация оказывается полностью управляемой
|
>> |
A = [0 1; -6 -5]; |
|
>> |
b = [0; 1]; |
|
>> |
det( |
|
|
ans = |
|
|
-1 |
|
>> |
UNC = length(A) – rank( |
|
|
UNC = |
|
|
0 |
При
использовании грамиана управляемости (5) получаем в Octave
для первой канонической формы
|
>> |
A = [0 1; -6 -5]; |
|
>> |
b |
|
>> |
syms |
|
>> |
U = expm(A*t)*b; |
|
>> |
U = int(U*U’, 0, int); |
|
>> |
det(w) |
|
|
ans = |
|
|
0 |
Реализация
не полностью управляемая.
Для
управляемой канонической формы в Octave
получаем
|
>> |
A = [0 1; -6 -5]; |
|
>> |
B = [0; 1]; |
|
>> |
syms t |
|
>> |
U = expm(A*t)*b; |
|
>> |
w = int(U*U’, 0, int); |
|
>> |
det(w) |
|
|
ans = |
|
|
1/500 |
Определитель
отличен от нуля — реализация полностью управляемая.
Совершенно
аналогично проверяется свойство наблюдаемости динамических систем с
использованием матрицы наблюдаемости или грамиана наблюдаемости. Таким образом Octave
легко используется для полного рассмотрения свойств управляемости и
наблюдаемости систем, заданных управлениями в пространстве состояний.
Список
литературы:
1. Дорф
Р., Бишоп Р. Современные системы управления. – М.: БИНОМ. Лаборатория знаний.
2009.- 832 с.
2. Капалин
В. И., Ильин В. А. Частотные методы теории управления в Octave.
Сборник научных трудов научно-технической конференции CITCONF
“Современные информационные технологии 2019”, 2019, ПГУ, Пенза. – 4с